
已知函数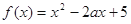 (
(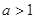 ).
).
(1)若 的定义域和值域均是
的定义域和值域均是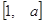 ,求实数
,求实数 的值;
的值;
(2)若对任意的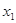 ,
,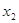
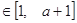 ,总有
,总有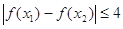 ,求实数
,求实数 的取值范围.
的取值范围.
(1)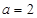 ;(2)
;(2)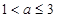
解析试题分析:(1)求出二次函数的对称轴是关键.通过对称轴知道函数f(x)在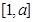 上单调递减.在结合已知条件即可得两个等式.求出结论.
上单调递减.在结合已知条件即可得两个等式.求出结论.
(2)条件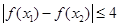 表示的含义是函数f(x)在
表示的含义是函数f(x)在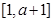 上的最大值与最小值的差小于或等于4.因为函数f(x)的对称轴为
上的最大值与最小值的差小于或等于4.因为函数f(x)的对称轴为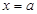 .所以要将
.所以要将 的值分两类
的值分两类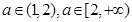 .再根据单调性即可求得
.再根据单调性即可求得 的范围.本题的函数的背景是二次函数所以抓住对称轴展开研究函数的最值单调性.同时分类的思想是解题的关键.
的范围.本题的函数的背景是二次函数所以抓住对称轴展开研究函数的最值单调性.同时分类的思想是解题的关键.
试题解析:(1)因为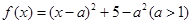 .所以f(x)在
.所以f(x)在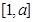 是减函数,又定义域和值域为
是减函数,又定义域和值域为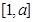 所以
所以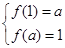 .即
.即 .解得
.解得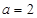 .
.
(2)若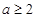 .又
.又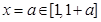 ,且
,且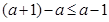 .所以
.所以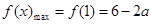 .
.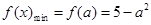 .因为对任意的
.因为对任意的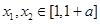 .总有
.总有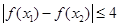 .所以
.所以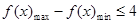 .即
.即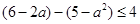 .解得
.解得 .又
.又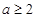 .所以
.所以 .若
.若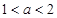 .
.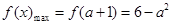 .
.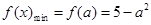 .
.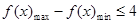 显然成立.综上
显然成立.综上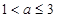 .
.
考点:1.二次函数的对成性.2.函数的最值问题.3.分类思想想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为 米,圆心角为
米,圆心角为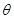 (弧度).
(弧度).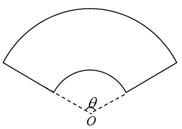
(1)求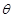 关于
关于 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,求
,求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 为何值时,
为何值时, 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如果函数 满足在集合
满足在集合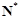 上的值域仍是集合
上的值域仍是集合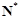 ,则把函数
,则把函数 称为N函数.
称为N函数.
例如: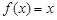 就是N函数.
就是N函数.
(Ⅰ)判断下列函数:①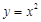 ,②
,②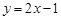 ,③
,③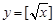 中,哪些是N函数?(只需写出判断结果);
中,哪些是N函数?(只需写出判断结果);
(Ⅱ)判断函数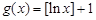 是否为N函数,并证明你的结论;
是否为N函数,并证明你的结论;
(Ⅲ)证明:对于任意实数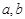 ,函数
,函数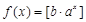 都不是N函数.
都不是N函数.
(注:“ ”表示不超过
”表示不超过 的最大整数)
的最大整数)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,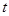 小时内供水总量为
小时内供水总量为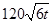 吨(
吨(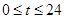 ),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
),从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经市场调查,某种商品在过去50天的销售量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=-2t+200(1≤t≤50,t∈N).前30天价格为g(t)=t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
(1)写出该种商品的日销售额S与时间t的函数关系;
(2)求日销售额S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com