
设 ,两个函数
,两个函数 ,
, 的图像关于直线
的图像关于直线 对称.
对称.
(1)求实数 满足的关系式;
满足的关系式;
(2)当 取何值时,函数
取何值时,函数 有且只有一个零点;
有且只有一个零点;
(3)当 时,在
时,在 上解不等式
上解不等式 .
.
(1)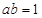 ;(2)
;(2)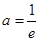 ;(3)
;(3)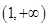 .
.
解析试题分析:(1)两个函数的图象关于某条直线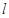 对称,一般都是设
对称,一般都是设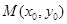 是一个函数图象上的任一点,求出这个点
是一个函数图象上的任一点,求出这个点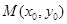 关于直线
关于直线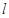 对称的点
对称的点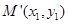 ,而点
,而点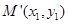 就在第二个函数的图象上,这样就把两个函数建立了联系;(2)函数
就在第二个函数的图象上,这样就把两个函数建立了联系;(2)函数 有且只有一个零点,一般是求
有且只有一个零点,一般是求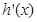 ,通过
,通过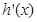 讨论函数
讨论函数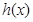 的单调性,最值,从而讨论零点的个数,当然本题中由于
的单调性,最值,从而讨论零点的个数,当然本题中由于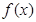 与
与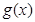 的图象关于直线
的图象关于直线 对称,因此
对称,因此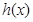 的唯一零点也就是它们的的唯一交点必在直线
的唯一零点也就是它们的的唯一交点必在直线 上,这个交点是函数
上,这个交点是函数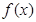 图象与直线
图象与直线 的切点,这样我们可从切线方面来解决问题;(3)考虑
的切点,这样我们可从切线方面来解决问题;(3)考虑
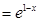
 ,
,
当然要解不等式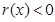 ,还需求
,还需求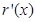 ,讨论
,讨论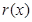 的单调性,极值,从而确定不等式的解集.
的单调性,极值,从而确定不等式的解集.
试题解析:(1)设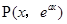 是函数
是函数 图像上任一点,则它关于直线
图像上任一点,则它关于直线 对称的点
对称的点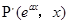 在函数
在函数 的图像上,
的图像上,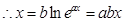 ,
,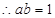 .
.
(2)当 时,函数
时,函数 有且只有一个零点,两个函数的图像有且只有一个交点,
有且只有一个零点,两个函数的图像有且只有一个交点,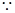 两个函数关于直线
两个函数关于直线 对称,
对称,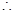 两个函数图像的交点就是函数
两个函数图像的交点就是函数 ,的图像与直线
,的图像与直线 的切点.
的切点.
设切点为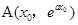 ,
,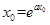
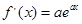 ,
,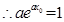 ,
,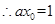 ,
,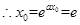 ,
,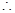 当
当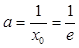 时,函数
时,函数 有且只有一个零点
有且只有一个零点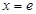 ;
;
(3)当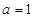 时,设
时,设 
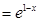
 ,则
,则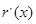
 ,当
,当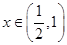 时,
时,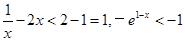 ,
,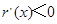 ,
,
当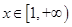 时,
时,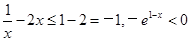 ,
,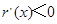 .
.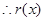 在
在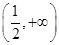 上是减函数.
上是减函数.
又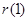 =0,
=0,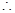 不等式
不等式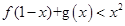 解集是
解集是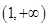 .
.
考点:(1)两个函数图象的对称问题;(2)函数的零点与切线问题;(3)解函数不等式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知函数 的定义域为
的定义域为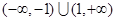 ,对定义域内的任意x,满足
,对定义域内的任意x,满足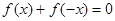 ,当
,当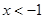 时,
时,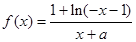 (a为常),且
(a为常),且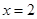 是函数
是函数 的一个极值点,
的一个极值点,
(1)求实数a的值;
(2)如果当 时,不等式
时,不等式 恒成立,求实数m的最大值;
恒成立,求实数m的最大值;
(3)求证: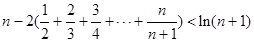
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式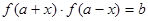 对定义域中的每一个
对定义域中的每一个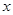 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.
(1) 判断函数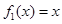 是否为“(
是否为“( )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数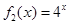 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对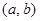 ;
;
(3)已知函数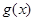 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对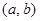 为(1,4).当
为(1,4).当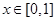 时,
时,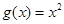
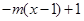
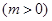 ,若当
,若当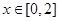 时,都有
时,都有 ,试求
,试求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.
(1)如果瓶内的药液恰好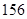 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?
(2)在条件(1)下,设输液开始后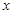 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为 (单位:厘米),已知当
(单位:厘米),已知当 时,
时,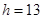 .试将
.试将 表示为
表示为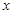 的函数.(注:
的函数.(注: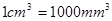 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 的导函数的图像与直线
的导函数的图像与直线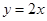 平行,且
平行,且 在
在 处取得极小值
处取得极小值 .设
.设 .
.
(1)若曲线 上的点
上的点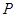 到点
到点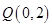 的距离的最小值为
的距离的最小值为 ,求
,求 的值;
的值;
(2)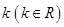 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
运货卡车以每小时 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米
 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用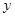 关于
关于 的表达式;
的表达式;
(2)当 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校课外兴趣小组的学生为了给学校边的一口被污染的池塘治污,他们通过实验后决定在池塘中投放一种能与水中的污染物质发生化学反应的药剂.已知每投放 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度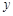 (克/升)随着时间
(克/升)随着时间 (天)变化的函数关系式近似为
(天)变化的函数关系式近似为 ,其中
,其中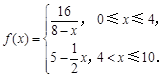 若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
若多次投放,则某一时刻水中的药剂浓度为各次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
(Ⅰ)若一次投放4个单位的药剂,则有效治污时间可达几天?
(Ⅱ)若第一次投放2个单位的药剂,6天后再投放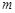 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求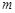 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com