
【题目】已知椭圆 ![]() 的一个焦点与抛物线
的一个焦点与抛物线 ![]() 的焦点
的焦点 ![]() 重合,且点
重合,且点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() ,
, ![]() 与
与 ![]() 的公共弦长为
的公共弦长为 ![]() .
.
(1)求椭圆 ![]() 的方程及点
的方程及点 ![]() 的坐标;
的坐标;
(2)过点 ![]() 的直线
的直线 ![]() 与
与 ![]() 交于
交于 ![]() 两点,与
两点,与 ![]() 交于
交于 ![]() 两点,求
两点,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:∵ ![]() 的焦点
的焦点 ![]() 的坐标为
的坐标为 ![]() ,
,
由点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() 得
得 ![]() .
.
∵ ![]() ,解得
,解得 ![]() ,又
,又 ![]() 为椭圆的一个焦点,∴
为椭圆的一个焦点,∴ ![]() .
.
∵ ![]() 与
与 ![]() 的公共弦长为
的公共弦长为 ![]() ,
, ![]() 与
与 ![]() 都关于
都关于 ![]() 轴对称,
轴对称,
而 ![]() 的方程为
的方程为 ![]() ,从而
,从而 ![]() 与
与 ![]() 的公共点的坐标为
的公共点的坐标为 ![]() ,
,
∴ ![]() ②,
②,
联立①②解得 ![]() ,
,
∴ ![]() 的方程为
的方程为 ![]() ,点
,点 ![]() 的坐标为
的坐标为 ![]()
(2)解:当 ![]() 过点
过点 ![]() 且垂直于
且垂直于 ![]() 轴时,
轴时, ![]() 的方程为
的方程为 ![]() 代入
代入 ![]() 求得
求得 ![]() ,
,
∴ ![]() ,把
,把 ![]() 代入
代入 ![]() 求得
求得 ![]() ,∴
,∴ ![]() ,
,
此时 ![]() .
.
当 ![]() 与
与 ![]() 轴不垂直时,要使
轴不垂直时,要使 ![]() 与
与 ![]() 有两个交点,可设
有两个交点,可设 ![]() 的方程为
的方程为 ![]() ,
,
此时设 ![]()
把直线 ![]() 的方程与椭圆
的方程与椭圆 ![]() 的方程联立得
的方程联立得 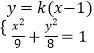 ,
,
消去 ![]() 化简得
化简得 ![]() ,
,
可得 ![]() ,
,
∴ ![]() ,
,
把直线 ![]() 的方程与抛物线
的方程与抛物线 ![]() 的方程联立得
的方程联立得 ![]() ,
,
消去 ![]() 化简得
化简得 ![]() ,
,
可得 ![]() ,
,
∴ ![]() ,
,
![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
,
综上可得 ![]() 的取值范围是
的取值范围是 ![]()
【解析】(1)由已知求出抛物线的焦点可得出 ![]() ,再利用点到直线的距离公式
,再利用点到直线的距离公式![]() 求得c的值,进而得到焦点的坐标然后求出抛物线的方程,再由已知再设出公共端点的坐标利用弦长公式 代入数值求出交点坐标,然后把数值带入到椭圆的方程计算得出a、b的值进而得到椭圆的方程。(2)由题意结合直线点斜式设出直线的方程,代入到抛物线的方程和椭圆的方程消去y得到的关于x的一元二次方程,利用韦达定理
求得c的值,进而得到焦点的坐标然后求出抛物线的方程,再由已知再设出公共端点的坐标利用弦长公式 代入数值求出交点坐标,然后把数值带入到椭圆的方程计算得出a、b的值进而得到椭圆的方程。(2)由题意结合直线点斜式设出直线的方程,代入到抛物线的方程和椭圆的方程消去y得到的关于x的一元二次方程,利用韦达定理![]() 和弦长公式
和弦长公式![]() 即可求得
即可求得![]() 的代数式,把结果代入到要求的式子里结合该式子的特点整理即可求出上式的取值范围。
的代数式,把结果代入到要求的式子里结合该式子的特点整理即可求出上式的取值范围。


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kex﹣x2(其中k∈R,e是自然对数的底数).
(Ⅰ)若k<0,试判断函数f(x)在区间(0,+∞)上的单调性;
(Ⅱ)若k=2,当x∈(0,+∞)时,试比较f(x)与2的大小;
(Ⅲ)若函数f(x)有两个极值点x1 , x2(x1<x2),求k的取值范围,并证明0<f(x1)<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以![]() 表示值域为R的函数组成的集合,
表示值域为R的函数组成的集合,![]() 表示具有如下性质的函数
表示具有如下性质的函数![]() 组成的集合:对于函数
组成的集合:对于函数![]() ,存在一个正数
,存在一个正数![]() ,使得函数
,使得函数![]() 的值域包含于区间
的值域包含于区间![]() .例如,当
.例如,当![]() ,
,![]() 时,
时,![]() ,
,![]() .现有如下命题:
.现有如下命题:
①设函数![]() 的定义域为
的定义域为![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ,
,![]() ,
,![]() ”;
”;
②函数![]() 的充要条件是
的充要条件是![]() 有最大值和最小值;
有最大值和最小值;
③若函数![]() ,
,![]() 的定义域相同,且
的定义域相同,且![]() ,
,![]() ,则
,则![]() ;
;
④若函数![]() (
(![]() ,
,![]() )有最大值,则
)有最大值,则![]() .
.
其中的真命题有 .(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高二年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下: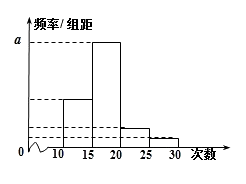

(1)求出表中M,P及图中 ![]() 的值;
的值;
(2)若该校高二学生有240人,试估计该校高二学生参加社区服务的次数在区间[10,15]内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[25,30]内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,已知曲线
中,已知曲线 ![]() :
: ![]() (
( ![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系 ![]() 的原点
的原点 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线 ![]() :
: ![]() .
.
(1)将曲线 ![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 ![]() 、2倍后得到曲线
、2倍后得到曲线 ![]() ,试写出直线
,试写出直线 ![]() 的直角坐标方程和曲线
的直角坐标方程和曲线 ![]() 的参数方程;
的参数方程;
(2)在曲线 ![]() 上求一点
上求一点 ![]() ,使点
,使点 ![]() 到直线
到直线 ![]() 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地电影院为了了解当地影迷对快要上映的一部电影的票价的看法,进行了一次调研,得到了票价x(单位:元)与渴望观影人数y(单位:万人)的结果如下表:
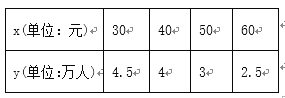
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据(1)中求出的线性回归方程,若票价定为70元,预测该电影院渴望观影人数.附:回归直线的斜率和截距的最小二乘法估计公式分别为: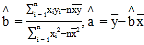
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点O,焦点在x轴上的椭圆,离心率 ![]() ,且椭圆过点
,且椭圆过点 ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)椭圆左,右焦点分别为F1 , F2 , 过F2的直线l与椭圆交于不同的两点A、B,则△F1AB的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,其中b≠c,且bcosB=ccosC,延长线段BC到点D,使得BC=4CD=4,∠CAD=30°, 
(Ⅰ)求证:∠BAC是直角;
(Ⅱ)求tan∠D的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com