Question

【题目】设集合A、B均为实数集R的子集，记：A+B={a+b|a∈A，b∈B}；
（1）已知A={0，1，2}，B={﹣1，3}，试用列举法表示A+B；
（2）设a1= ，当n∈N* ， 且n≥2时，曲线 的焦距为an ， 如果A={a1 ， a2 ， …，an}，B= ，设A+B中的所有元素之和为Sn ， 对于满足m+n=3k，且m≠n的任意正整数m、n、k，不等式Sm+Sn﹣λSk＞0恒成立，求实数λ的最大值；
（3）若整数集合A1A1+A1 ， 则称A1为“自生集”，若任意一个正整数均为整数集合A2的某个非空有限子集中所有元素的和，则称A2为“N*的基底集”，问：是否存在一个整数集合既是自生集又是N*的基底集？请说明理由．

Answer 1

【答案】
（1）解：∵A+B={a+b|a∈A，b∈B}；

当A={0，1，2}，B={﹣1，3}时，

A+B={﹣1，0，1，3，4，5}

（2）解：曲线 ，即 ，在n≥2时表示双曲线，

故an=2 = ，

∴a1+a2+a3+…+an= ，

∵B= ，

∴A+B中的所有元素之和为Sn=3（a1+a2+a3+…+an）+n（ ）=3 ﹣m=n2，

∴Sm+Sn﹣λSk＞0恒成立， ＞λ恒成立，

∵m+n=3k，且m≠n，

∴ = = ＞ ，

∴ ，

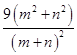即实数λ的最大值为

（3）解：存在一个整数集合既是自生集又是N*的基底集，理由如下：

设整数集合A={x|x=（﹣1）nFn，n∈N*，n≥2}，其中{Fn}为斐波那契数列，

即F1=F2=1，Fn+2=Fn+Fn+1，n∈N*，

下证：整数集合A既是自生集又是N*的基底集，

①由Fn=Fn+2﹣Fn+1得：（﹣1）nFn=（﹣1）n+2Fn+2+（﹣1）n+1Fn+1，

故A是自生集；

②对于任意n≥2，对于任一正整数t∈[1，F2n+1﹣1]，存在集合Ar一个有限子集{a1，a2，…，am}，

使得t=a1+a2+…+am，（|ai＜F2n+1，i=1，2，…，m），

当n=2时，由1=1，2=3+1﹣2，3=3，4=3+1，知结论成立；

假设结论对n=k时成立，

则n=k+1时，只须对任何整数m∈[F2k+1，F2k+3]讨论，

若m＜F2k+2，则m=F2k+2+ ， ∈（﹣F2k+1，0），

故 =﹣F2k+1+m′，m′∈[1，F2k+1），

由归纳假设，m′可以表示为集合A中有限个绝对值小于F2k+1的元素的和．

因为m=F2k+2﹣F2k+1+m′=（﹣1）2k+2F2k+2+（﹣1）2k+1F2k+1+m′，

所以m可以表示为集合A中有限个绝对值小于F2k+3的元素的和．

若m=F2k+2，则结论显然成立．

若F2k+2＜m＜F2k+3，则m=F2k+2+m′，m′∈[1，F2k+1），

由归纳假设知，m可以表示为集合A中有限个绝对值小于F2k+3的元素的和．

所以，当n=k+1时结论也成立；

由于斐波那契数列是无界的，

所以，任一个正整数都可以表示成集合A的一个有限子集中所有元素的和．

因此集合A又是N*的基底集

【解析】（1）根据新定义A+B={a+b|a∈A，b∈B}，结合已知中的集合A，B，可得答案；（2）曲线 表示双曲线，进而可得an= ，Sn=n2 ， 则Sm+Sn﹣λSk＞0恒成立， ＞λ恒成立，结合m+n=3k，且m≠n，及基本不等式，可得 ＞ ，进而得到答案；（3）存在一个整数集合既是自生集又是N*的基底集，结合已知中“自生集”和“N*的基底集”的定义，可证得结论；