
【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)设![]() ,求证:数列
,求证:数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对于
对于![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() 的最小值为3.
的最小值为3.
【解析】试题分析:(1)利用递推公式即可得出![]() 为一个常数,从而证明数列
为一个常数,从而证明数列![]() 是等差数,再利用等差数列的通项公式即可得到
是等差数,再利用等差数列的通项公式即可得到![]() ,进而得到
,进而得到![]() ;(2)利用(1)的结论,利用“裂项求和”即可得到
;(2)利用(1)的结论,利用“裂项求和”即可得到![]() ,要使得
,要使得![]() 对于
对于![]() 恒成立,只要
恒成立,只要![]() ,即
,即![]() ,解出即可.
,解出即可.
试题解析:(1)证明: 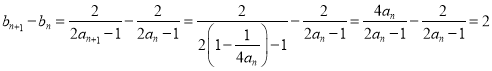 ,
,
所以数列![]() 是等差数列,
是等差数列,
![]() ,因此
,因此![]() ,
,
由![]() .
.
(2)由![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() 恒成立,
恒成立,
依题意要使![]() 对于
对于![]() ,恒成立,只需
,恒成立,只需![]() ,且
,且![]() 解得
解得![]() ,
, ![]() 的最小值为
的最小值为![]() .
.
【方法点晴】裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,掌握一些常见的裂项技巧:①![]() ;②
;②![]()
![]() ;③
;③![]() ;
;
④![]()
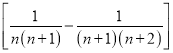 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,
=(1, ![]() ),
), ![]() =(sinx,cosx),设函数f(x)=
=(sinx,cosx),设函数f(x)= ![]()
![]()
(1)求函数f(x)的最小正周期和最大值;
(2)设锐角△ABC的三个内角A,B,C的对边分别为a,b,c,若c= ![]() ,cosB=
,cosB= ![]() ,且f(C)=
,且f(C)= ![]() ,求b.
,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解2013年某校高三学生的视力情况,随机抽查了一部分学生视力,将调查结果分组,分组区间为![]() ,
,![]() ,… ,
,… ,![]() 经过数据处理,得到如右频率分布表:
经过数据处理,得到如右频率分布表:
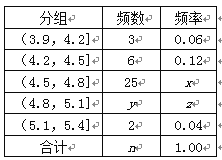
(1)求频率分布表中未知量![]() 的值;
的值;
(2)从样本中视力在![]() 和
和![]() 的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线上横坐标为
,抛物线上横坐标为![]() 的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
的点到抛物线顶点的距离与该点到抛物线准线的距离相等。
(1)求抛物线![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某成衣批发店为了对一款成衣进行合理定价,将该款成衣按事先拟定的价格进行试销,得到了如下数据:
批发单价x(元) | 80 | 82 | 84 | 86 | 88 | 90 |
销售量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() ,其中
,其中 ![]()
(2)预测批发单价定为85元时,销售量大概是多少件?
(3)假设在今后的销售中,销售量与批发单价仍然服从(1)中的关系,且该款成衣的成本价为40元/件,为使该成衣批发店在该款成衣上获得更大利润,该款成衣单价大约定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产产品过程中记录的产量x(吨)与相应的生产能耗y(吨)标准煤的几组对照数据:
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)求y关于x的线性回归方程;(已知 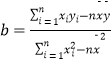 )
)
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低了多少吨标准煤.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如表数据:
单价x(元) | 18 | 19 | 20 | 21 | 22 |
销量y(册) | 61 | 56 | 50 | 48 | 45 |
(1)求试销5天的销量的方差和y对x的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,
为了获得最大利润,该单元卷的单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com