【题目】已知向量 
=（1， 
）， 
=（sinx，cosx），设函数f（x）=
（1）求函数f（x）的最小正周期和最大值；
（2）设锐角△ABC的三个内角A，B，C的对边分别为a，b，c，若c= 
，cosB= 
，且f（C）= ，求b．
【答案】
（1）解：f（x）=sinx+ 
cosx=2sin（x+ 
），
∴f（x）的最小正周期T=2π，f（x）的最大值为2
（2）解：∵f（C）=2sin（C+ ）= ，∴sin（C+ ）= 
，
∵0 
，∴C= ．
∵cosB= 
，∴sinB= 
．
由正弦定理得 
，∴ 
，
解得：b= 
．
【解析】（1）根据向量的数量积公式得出f（x）解析式，使用和角公式化简，结合正弦函数的性质得出答案；（2）根据f（C）= 得出C，根据同角三角函数的关系计算sinB，由正弦定理得出b．
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:
，以及对余弦定理的定义的理解，了解余弦定理:
;
;
．
永乾教育寒假作业快乐假期延边人民出版社系列答案科目：高中数学 来源： 题型：
【题目】已知圆C：x2＋y2＋2x－4y＋3＝0．
(1)若圆C的切线在x轴和y轴上的截距相等，求此切线的方程．
(2)从圆C外一点P(x1，y1)向该圆引一条切线，切点为M，O为坐标原点，且有|PM|＝|PO|，求使得|PM|取得最小值的点P的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
sin 
cos +sin2 （ω＞0，0＜φ＜ 
）．其图象的两个相邻对称中心的距离为 ，且过点（ 
，1）．
（1）函数f（x）的解析式；
（2）在△ABC中，角A，B，C所对的边分别为a，b，c．已知 
= 
．且f（A）= 
，求角C的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】学校为了解学生在课外读物方面的支出情况，抽取了n名同学进行调查，结果显示这些同学的支出都在[10,50)(单位：元)，其中支出在[30,50)(单位：元)的同学有67人，其频率分布直方图如图所示，则n的值为( )
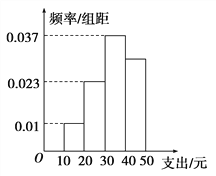
A. 100 B. 120 C. 130 D. 390
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】学校为了解学生在课外读物方面的支出情况，抽取了n名同学进行调查，结果显示这些同学的支出都在[10,50)(单位：元)，其中支出在[30,50)(单位：元)的同学有67人，其频率分布直方图如图所示，则n的值为( )
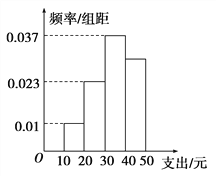
A. 100 B. 120 C. 130 D. 390
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况，从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高，数据如下：(单位：cm)
甲：9,10,11,12,10,20
乙：8,14,13,10,12,21.
(1)在给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图；
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差，并由此判断甲、乙两种麦苗的长势情况．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
满足
， 
，其中
.
（1）设
，求证：数列
是等差数列，并求出
的通项公式；
（2）设
，数列
的前
项和为
，是否存在正整数
，使得
对于
恒成立，若存在，求出
的最小值，若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷，按事先拟定的价格进行5天试销，每种单价试销1天，得到如下数据：
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
（1）求试销5天的销量的方差和
对
的回归直线方程；
（2）预计今后的销售中，销量与单价服从（1）中的回归方程，已知每册单元卷的成本是14元，为了获得最大利润，该单元卷的单价卷的单价应定为多少元？
（附：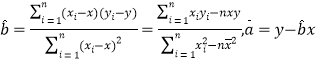
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=Asin（x+φ）（A＞0，0＜φ＜π），x∈R的最大值是1，其图象经过点 
．
（1）求f（x）的解析式；
（2）已知 
，且 
， 
，求f（α﹣β）的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com