
设 (
(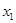 ,
,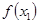 ),
), (
( ,
,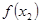 )是函数
)是函数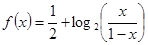 的图象上的任意两点.
的图象上的任意两点.
(1)当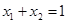 时,求
时,求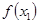 +
+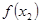 的值;
的值;
(2)设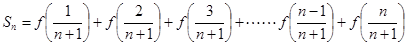 ,其中
,其中 ,求
,求
(3)对应(2)中 ,已知
,已知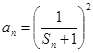 ,其中
,其中 ,设
,设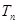 为数列
为数列 的前
的前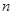 项和,求证
项和,求证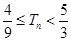 .
.
(1)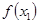 +
+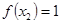 ;(2)
;(2)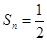 ;(3)
;(3)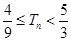
解析试题分析:(1)熟练地运用对数的三个运算性质并配以代数式的恒等变换是对数的计算、化简、证明的常用技巧;(2)若前后项的和相加为定值,则采用倒序相加法求数列的和,其基本思想和等差数列的前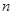 项和相类似;(3)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的;(4)不等式具有放缩功能,常常用于证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好切入点.
项和相类似;(3)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的;(4)不等式具有放缩功能,常常用于证明不等式,解决问题的关键是分析不等式两边的结构特点,选择好切入点.
试题解析:解:(1)
 且
且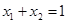
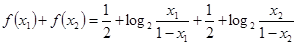
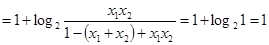
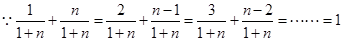
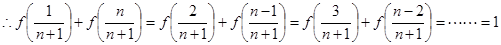

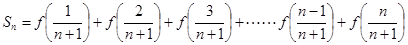
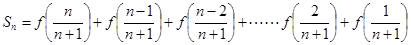
+(2)得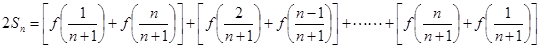
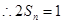 ,解得
,解得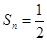
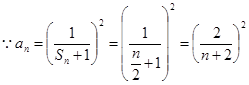
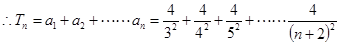
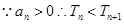 ,
,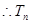 是单调递减数列
是单调递减数列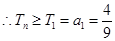
又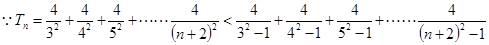
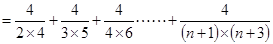
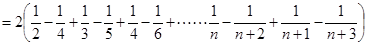
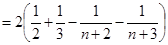

 综上所述:
综上所述: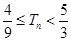
考点:(1)对数的运算性质;(2)倒序相加求数列的和;(3)证明不等式.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com