
已知数列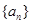 的前
的前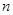 项和
项和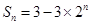 ,则
,则 .
.
 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:填空题
下列命题中,真命题的序号是 .
①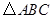 中,
中,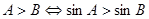
②数列{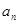 }的前n项和
}的前n项和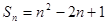 ,则数列{
,则数列{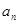 }是等差数列.
}是等差数列.
③锐角三角形的三边长分别为3,4,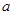 ,则
,则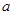 的取值范围是
的取值范围是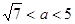 .
.
④等差数列{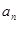 }前n项和为
}前n项和为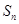 。已知
。已知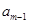 +
+ -
-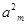 =0,
=0,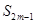 =38,则m=10.
=38,则m=10.
⑤常数数列既是等差数列又是等比数列.
⑥数列{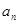 }满足,
}满足,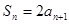 ,则数列{
,则数列{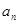 }为等比数列.
}为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
五位同学围成一圈依次循环报数,规定,第一位同学首次报出的数为1,第二位同学首次报出的数为2,之后每位同学所报出的数都是前两位同学所报出数的乘积的个位数字,则第2013个被报出的数为
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在如图所示的数表中,第i行第j列的数记为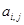 ,且满足
,且满足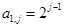 ,
,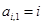 ,
, (
(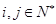 );又记第3行的数3,5,8,13,22,39……为数列{bn},则
);又记第3行的数3,5,8,13,22,39……为数列{bn},则
(1)此数表中的第2行第8列的数为_________.
(2)数列{bn}的通项公式为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
[2014·河北教学质量监测]已知数列{an}满足:a1=1,an+1=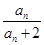 (n∈N*).若bn+1=(n-λ)(
(n∈N*).若bn+1=(n-λ)(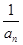 +1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( )
+1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( )
| A.λ>2 | B.λ>3 | C.λ<2 | D.λ<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com