
下列命题中,真命题的序号是 .
①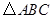 中,
中,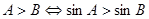
②数列{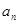 }的前n项和
}的前n项和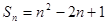 ,则数列{
,则数列{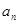 }是等差数列.
}是等差数列.
③锐角三角形的三边长分别为3,4,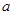 ,则
,则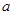 的取值范围是
的取值范围是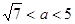 .
.
④等差数列{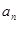 }前n项和为
}前n项和为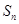 。已知
。已知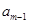 +
+ -
-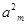 =0,
=0,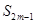 =38,则m=10.
=38,则m=10.
⑤常数数列既是等差数列又是等比数列.
⑥数列{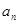 }满足,
}满足,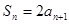 ,则数列{
,则数列{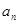 }为等比数列.
}为等比数列.
科目:高中数学 来源: 题型:填空题
设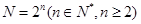 ,将
,将 个数
个数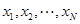 依次放入编号为1,2,…,
依次放入编号为1,2,…, 的
的 个位置,得到排列
个位置,得到排列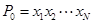 ,将该排列中分别位于奇数与偶数位置的数取出,并按原顺序依次放入对应的前
,将该排列中分别位于奇数与偶数位置的数取出,并按原顺序依次放入对应的前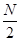 和后
和后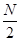 个位置,得到排列
个位置,得到排列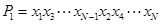 ,将此操作称为
,将此操作称为 变换,将
变换,将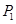 分成两段,每段
分成两段,每段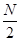 个数,并对每段作
个数,并对每段作 变换,得到
变换,得到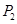 ;当
;当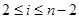 时,将
时,将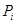 分成
分成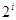 段,每段
段,每段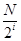 个数,并对每段作
个数,并对每段作 变换,得到
变换,得到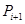 ,例如,当
,例如,当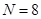 时,
时,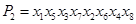 ,此时,
,此时,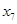 位于
位于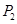 中的第4个位置.当
中的第4个位置.当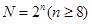 时,
时,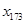 位于
位于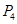 中的第 个位置.
中的第 个位置.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
挪威数学家阿贝尔,曾经根据阶梯形图形的两种不同分割(如下图),利用它们的面积关系发现了一个重要的恒等式——阿贝尔公式: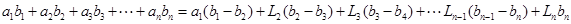
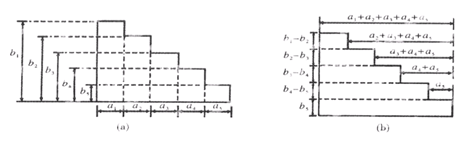
则其中:(I)L3= ;(Ⅱ)Ln= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com