
已知数列 中,
中,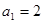 ,对
,对 总有
总有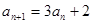 成立,
成立,
(1)计算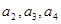 的值;
的值;
(2)根据(1)的结果猜想数列的通项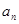 ,并用数学归纳法证明
,并用数学归纳法证明
科目:高中数学 来源: 题型:填空题
五位同学围成一圈依次循环报数,规定,第一位同学首次报出的数为1,第二位同学首次报出的数为2,之后每位同学所报出的数都是前两位同学所报出数的乘积的个位数字,则第2013个被报出的数为
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列 的前n项和为
的前n项和为 ,
, ,且
,且 (
( ),数列
),数列 满足
满足 ,
, ,对任意
,对任意 ,都有
,都有 。
。
(1)求数列 、
、 的通项公式;
的通项公式;
(2)令 .
.
①求证: ;
;
②若对任意的 ,不等式
,不等式 恒成立,试求实数λ的取值范围.
恒成立,试求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列{an}的通项公式为an=n2-n-30.
(1)求数列的前三项,60是此数列的第几项?
(2)n为何值时,an=0,an>0,an<0?
(3)该数列前n项和Sn是否存在最值?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分18分)本题共3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知数列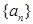 满足
满足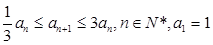 .
.
(1)若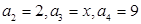 ,求
,求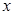 的取值范围;
的取值范围;
(2)若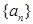 是等比数列,且
是等比数列,且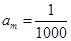 ,正整数
,正整数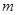 的最小值,以及
的最小值,以及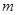 取最小值时相应
取最小值时相应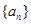 的仅比;
的仅比;
(3)若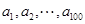 成等差数列,求数列
成等差数列,求数列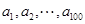 的公差的取值范围.
的公差的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于数列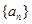 ,把
,把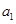 作为新数列
作为新数列 的第一项,把
的第一项,把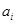 或
或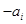 (
(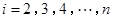 )作为新数列
)作为新数列 的第
的第 项,数列
项,数列 称为数列
称为数列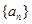 的一个生成数列.例如,数列
的一个生成数列.例如,数列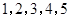 的一个生成数列是
的一个生成数列是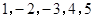 .已知数列
.已知数列 为数列
为数列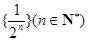 的生成数列,
的生成数列,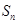 为数列
为数列 的前
的前 项和.
项和.
(1)写出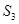 的所有可能值;
的所有可能值;
(2)若生成数列 满足
满足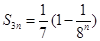 ,求数列
,求数列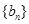 的通项公式;
的通项公式;
(3)证明:对于给定的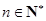 ,
,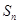 的所有可能值组成的集合为
的所有可能值组成的集合为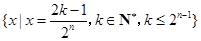 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
[2014·河北教学质量监测]已知数列{an}满足:a1=1,an+1=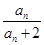 (n∈N*).若bn+1=(n-λ)(
(n∈N*).若bn+1=(n-λ)(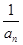 +1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( )
+1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( )
| A.λ>2 | B.λ>3 | C.λ<2 | D.λ<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com