
对于数列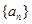 ,把
,把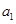 作为新数列
作为新数列 的第一项,把
的第一项,把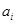 或
或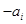 (
(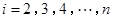 )作为新数列
)作为新数列 的第
的第 项,数列
项,数列 称为数列
称为数列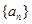 的一个生成数列.例如,数列
的一个生成数列.例如,数列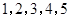 的一个生成数列是
的一个生成数列是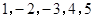 .已知数列
.已知数列 为数列
为数列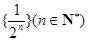 的生成数列,
的生成数列,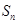 为数列
为数列 的前
的前 项和.
项和.
(1)写出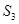 的所有可能值;
的所有可能值;
(2)若生成数列 满足
满足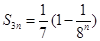 ,求数列
,求数列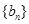 的通项公式;
的通项公式;
(3)证明:对于给定的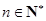 ,
,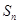 的所有可能值组成的集合为
的所有可能值组成的集合为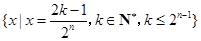 .
.
(1) (2)
(2)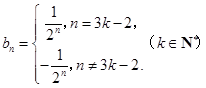 (3)详见解析.
(3)详见解析.
解析试题分析:(1)列举出数列 所有可能情况,共
所有可能情况,共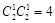 种,分别计算和值为
种,分别计算和值为 ,本题目的初步感观生成数列
,本题目的初步感观生成数列 (2)已知和项解析式,则可利用
(2)已知和项解析式,则可利用 求通项. 当
求通项. 当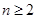 时,
时,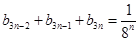 ,而
,而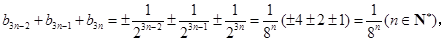 当且仅当
当且仅当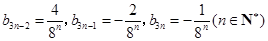 时,才成立.所以
时,才成立.所以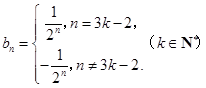 (3)本题实际是对(1)的推广.证明的实质是确定集合
(3)本题实际是对(1)的推广.证明的实质是确定集合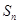 的个数及其表示形式.首先集合
的个数及其表示形式.首先集合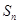 的个数最多有
的个数最多有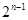 种情形,而每一种的值都不一样,所以个数为
种情形,而每一种的值都不一样,所以个数为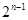 种情形,这是本题的难点,利用同一法证明. 确定集合
种情形,这是本题的难点,利用同一法证明. 确定集合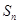 的表示形式,关键在于说明分子为奇数.由
的表示形式,关键在于说明分子为奇数.由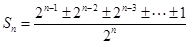 得分子必是奇数,奇数个数由范围
得分子必是奇数,奇数个数由范围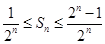 确定.
确定.
试题解析:解:(1)由已知, ,
,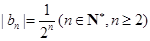 ,
,
∴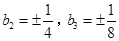 ,
,
由于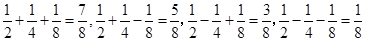 ,
,
∴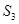 可能值为
可能值为 . 3分
. 3分
(2)∵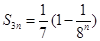 ,
,
当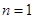 时,
时,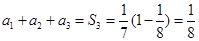 ,
,
当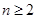 时,
时,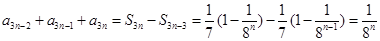 ,
,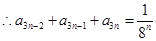 ,
, , 5分
, 5分
∵ 是
是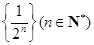 的生成数列,
的生成数列,
∴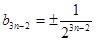 ;
;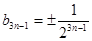 ;
;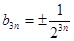 ;
;
∴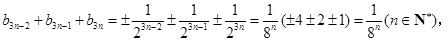
在以上各种组合中,
当且仅当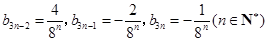 时,才成立.
时,才成立.
∴ . 8分
. 8分
(3)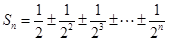 共有
共有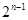 种情形.
种情形.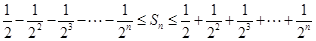 ,即
,即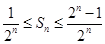 ,
,
又 ,分子必是奇数,
,分子必是奇数,
满足条件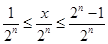 的奇数
的奇数 共有
共有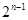 个. 10分
个. 10分
设数列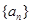 与数列
与数列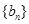 为两个生成数列,数列
为两个生成数列,数列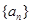 的前
的前 项和为
项和为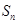 ,数列
,数列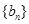 的前
的前 项和为
项和为 ,从第二项开始比较两个数列,设第一个不相等的项为第
,从第二项开始比较两个数列,设第一个不相等的项为第 项.
项.
由于 ,不妨设
,不妨设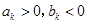 ,
,
则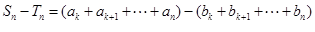
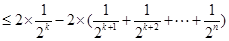
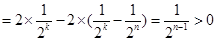


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
已知数列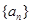 和
和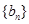 的通项公式分别为
的通项公式分别为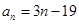 ,
,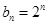 .将
.将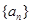 与
与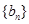 中的公共项按照从小到大的顺序排列构成一个新数列记为
中的公共项按照从小到大的顺序排列构成一个新数列记为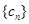 .
.
(1)试写出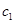 ,
,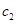 ,
,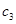 ,
,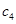 的值,并由此归纳数列
的值,并由此归纳数列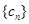 的通项公式;
的通项公式;
(2)证明你在(1)所猜想的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若数列{an}满足an+1=an+an+2(n∈N*),则称数列{an}为“凸数列”.
(1)设数列{an}为“凸数列”,若a1=1,a2=-2,试写出该数列的前6项,并求出前6项之和;
(2)在“凸数列”{an}中,求证:an+3=-an,n∈N*;
(3)设a1=a,a2=b,若数列{an}为“凸数列”,求数列前2011项和S2011.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若无穷数列 满足:①对任意
满足:①对任意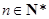 ,
,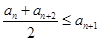 ;②存在常数
;②存在常数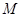 ,对任意
,对任意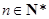 ,
,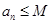 ,则称数列
,则称数列 为“
为“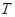 数列”.
数列”.
(Ⅰ)若数列 的通项为
的通项为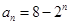
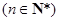 ,证明:数列
,证明:数列 为“
为“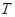 数列”;
数列”;
(Ⅱ)若数列 的各项均为正整数,且数列
的各项均为正整数,且数列 为“
为“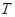 数列”,证明:对任意
数列”,证明:对任意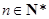 ,
,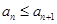 ;
;
(Ⅲ)若数列 的各项均为正整数,且数列
的各项均为正整数,且数列 为“
为“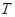 数列”,证明:存在
数列”,证明:存在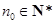 ,数列
,数列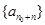 为等差数列.
为等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列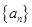 的通项公式为
的通项公式为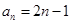 ,数列
,数列 的前
的前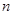 项和为
项和为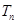 ,且满足
,且满足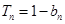 .
.
(1)求 的通项公式;
的通项公式;
(2)在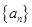 中是否存在使得
中是否存在使得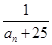 是
是 中的项,若存在,请写出满足题意的其中一项;若不存在,请说明理由.
中的项,若存在,请写出满足题意的其中一项;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com