
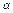 等于多少弧度时,这个扇形的面积最大?
等于多少弧度时,这个扇形的面积最大? -2,65°26′扇形的面积为S=
-2,65°26′扇形的面积为S= r2
r2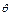 =
= (
( -2)r2
-2)r2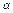 ="2" rad时,扇形的面积取最大值
="2" rad时,扇形的面积取最大值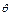 rad,因为扇形的弧长是r
rad,因为扇形的弧长是r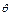 ,
,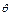 .
.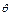 =
=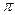 r,
r,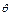 =
=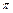 -2=(
-2=(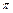 -2)×
-2)×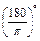
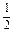 r2
r2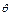 =
=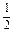 (
(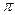 -2)r2.
-2)r2.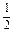 lr,将①代入,得
lr,将①代入,得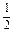 (20-2r)r=-r2+10r=-(r-5)2+25,
(20-2r)r=-r2+10r=-(r-5)2+25,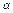 =
=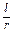 =2.
=2.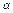 ="2" rad时,扇形的面积取最大值.
="2" rad时,扇形的面积取最大值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com