分析:(1)欲证CE⊥BD,而CE?平面ACC1A1,可先证BD⊥平面ACC1A1,根据直线与平面垂直的判定定理可知只需证BD与平面ACC1A1内两相交直线垂直,根据正方体的性质BD⊥AC,AA1⊥平面ABCD,BD?平面ABCD,则BD⊥AA1,又AC∩AA1=A,满足定理所需条件;
(2)欲证CE∥平面A1BD,根据直线与平面平行的判定定理可知只需证CE与平面A1BD内一直线平行,连接A1F,根据AA1∥BB1∥CC1,
AA1=BB1=CC1,可得ACC1A1为平行四边形,根据中位线可知CE∥FA1,FA1?面A1BD,CE?平面A1BD,满足定理所需条件;
(3)先求出正三角形△A1BD的面积,然后根据BC⊥平面A1B1BA,则BC⊥A1B,求出直角三角形△A1BC的面积,同理求出△A1CD的面积和△BCD面积,最后将四个面积相加即可.
解答:解:(1)证明:根据正方体的性质BD⊥AC,(2分)
因为AA
1⊥平面ABCD,BD?平面ABCD,所以BD⊥AA
1,
又AC∩AA
1=A,
所以BD⊥平面ACC
1A
1,CE?平面ACC
1A
1,所以CE⊥BD.(4分)
(2)证明:连接A
1F,因为AA
1∥BB
1∥CC
1,AA
1=BB
1=CC
1,
所以ACC
1A
1为平行四边形,
因此A
1C
1∥AC,A
1C
1=AC,
由于E是线段A
1C
1的中点,
所以CE∥FA
1,(6分)
因为FA
1?面A
1BD,CE?平面A
1BD,
所以CE∥平面A
1BD.(8分)
(3)△A
1BD是边长为
a的正三角形,
其面积为
S1=•(a)2=,(9分)
因为BC⊥平面A
1B
1BA,所以BC⊥A
1B,
所以△A
1BC是直角三角形,其面积为
S2=•a•a=a2,
同理△A
1CD的面积为
S3=S2=a2,(12分)
△BCD面积为
S4=a2.(13分)
所以三棱锥D-A
1BC的表面积为
S=S1+S2+S3+S4=a2.(14分)
点评:本小题主要考查直线与平面垂直的性质,直线与平面平行的判定,以及三棱锥的表面积等基础知识,考查空间想象能力、运算求解能力、推理论证能力,考查化归与转化思想,属于中档题.

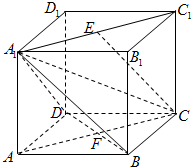 在棱长为a的正方体ABCD-A1B1C1D1中,E是线段A1C1的中点,AC∩BD=F.
在棱长为a的正方体ABCD-A1B1C1D1中,E是线段A1C1的中点,AC∩BD=F.

