
 A.(极坐标系与参数方程选做题) 已知圆ρ=3cosθ,则圆截直线
A.(极坐标系与参数方程选做题) 已知圆ρ=3cosθ,则圆截直线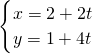 (t是参数)所得的弦长为________;
(t是参数)所得的弦长为________;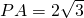 ,PC=1,则圆O的半径等于________.
,PC=1,则圆O的半径等于________. ,0),半径为
,0),半径为  ,直线
,直线 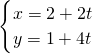 (t是参数)的直角坐标方程为:2x-y-3=0,直线经过圆心,所得的弦长为:3.
(t是参数)的直角坐标方程为:2x-y-3=0,直线经过圆心,所得的弦长为:3. :如图,连AO并延长,交圆O与另一点E,交割线PCB于点D,
:如图,连AO并延长,交圆O与另一点E,交割线PCB于点D,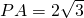 ,得AD=2,PD=4,而PC=1,
,得AD=2,PD=4,而PC=1,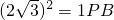 ,则PB=11,
,则PB=11,

科目:高中数学 来源: 题型:
 (A)(不等式选讲)不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则实数a的取值范围是
(A)(不等式选讲)不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则实数a的取值范围是查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| 2 |
| 5 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
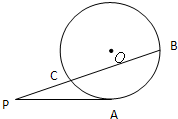 A.(极坐标系与参数方程选做题) 已知圆ρ=3cosθ,则圆截直线
A.(极坐标系与参数方程选做题) 已知圆ρ=3cosθ,则圆截直线
|
| 3 |
查看答案和解析>>
科目:高中数学 来源:2011年广东省中山一中高三第八次统测数学试卷(理科)(解析版) 题型:解答题
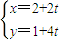 (t是参数)所得的弦长为 ;
(t是参数)所得的弦长为 ; ,PC=1,则圆O的半径等于 .
,PC=1,则圆O的半径等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com