
 ,
, ,
, ,
, +
+ =
= .
. •
• =
= .所以2个孩子中至少有一个显性决定特征的概率为1-
.所以2个孩子中至少有一个显性决定特征的概率为1- =
= .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
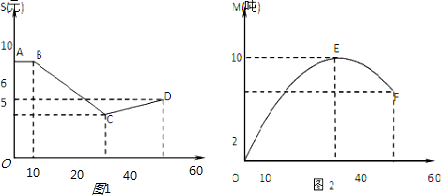
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx, sin2x),f(x)=
sin2x),f(x)=
 ,b=1,求角C.
,b=1,求角C.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
| 患胃病 | 未患胃病 | 合计 | |
| 生活无规律 | 5 | 15 | 20 |
| 生活有规律 | 40 | 10 | 50 |
| 合计 | 45 | 25 | 70 |
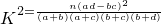
| P(K2≥k0) | 0.5 | 0.10 | 0.010 | 0.001 |
| k0 | 0.455 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
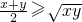 ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 =(2sinc,-
=(2sinc,- ),
), =(cos2c,
=(cos2c,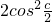 -1)且
-1)且 ∥
∥ .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com