
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asinB=﹣bsin(A+ ![]() ).
).
(1)求A;
(2)若△ABC的面积S= ![]() c2 , 求sinC的值.
c2 , 求sinC的值.
【答案】
(1)解:∵asinB=﹣bsin(A+ ![]() ).
).
∴由正弦定理可得:sinAsinB=﹣sinBsin(A+ ![]() ).即:sinA=﹣sin(A+
).即:sinA=﹣sin(A+ ![]() ).
).
可得:sinA=﹣ ![]() sinA﹣
sinA﹣ ![]() cosA,化简可得:tanA=﹣
cosA,化简可得:tanA=﹣ ![]() ,
,
∵A∈(0,π),
∴A= ![]()
(2)解:∵A= ![]() ,
,
∴sinA= ![]() ,
,
∵由S= ![]() c2=
c2= ![]() bcsinA=
bcsinA= ![]() bc,可得:b=
bc,可得:b= ![]() ,
,
∴a2=b2+c2﹣2bccosA=7c2,可得:a= ![]() ,
,
由正弦定理可得:sinC= ![]()
【解析】(1)由正弦定理化简已知可得tanA=﹣ ![]() ,结合范围A∈(0,π),即可计算求解A的值.(2)由(1)可求sinA=
,结合范围A∈(0,π),即可计算求解A的值.(2)由(1)可求sinA= ![]() ,利用三角形面积公式可求b=
,利用三角形面积公式可求b= ![]() ,利用余弦定理可求a=
,利用余弦定理可求a= ![]() ,由正弦定理即可计算求解.
,由正弦定理即可计算求解.
【考点精析】认真审题,首先需要了解正弦定理的定义(正弦定理:![]() ),还要掌握余弦定理的定义(余弦定理:
),还要掌握余弦定理的定义(余弦定理:![]() ;
;![]() ;
;![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直线坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为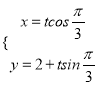 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的参数方程;
的参数方程;
(2)设点![]() 在
在![]() 上,
上, ![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直,求
垂直,求![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=2sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个周期后,所得图象对应的函数为( )
个周期后,所得图象对应的函数为( )
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin(2x﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.
(1)求a,b的值;
(2)讨论f(x)的单调性,并求f(x)的极大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区停车场的收费标准为:每车每次停车时间不超过2小时免费,超过2小时的部分每小时收费1元(不足1小时的部分按1小时计算).现有甲乙两人相互独立到停车场停车(各停车一次),且两人停车的时间均不超过5小时,设甲、乙两人停车时间(小时)与取车概率如下表所示:

(1)求甲、乙两人所付车费相同的概率;
(2)设甲、乙两人所付停车费之和为随机变量![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DBCE. 
(1)求证:△ADB∽△EAC;
(2)若∠BAC=40°,求∠DAE的度数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若偶函数f(x)在(﹣∞,﹣1]上是增函数,则下列关系式中成立的是( )
A.f(﹣ ![]() )<f(﹣1)<f(2)
)<f(﹣1)<f(2)
B.f(﹣1)<f(﹣ ![]() )<f(2)
)<f(2)
C.f(2)<f(﹣1)<f(﹣ ![]() )
)
D.f(2)<f(﹣ ![]() )<f(﹣1)
)<f(﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com