
【题目】已知正项数列{an}满足a1=1,(n+1)a2n+1+an+1an﹣na ![]() =0,数列{bn}的前n项和为Sn且Sn=1﹣bn .
=0,数列{bn}的前n项和为Sn且Sn=1﹣bn .
(1)求{an}和{bn}的通项;
(2)令cn= ![]() , ①求{cn}的前n项和Tn;
, ①求{cn}的前n项和Tn;
②是否存在正整数m满足m>3,c2 , c3 , cm成等差数列?若存在,请求出m;若不存在,请说明理由.
【答案】
(1)解:∵(n+1)a2n+1+an+1an﹣na ![]() =0,∴[(n+1)an+1﹣nan](an+1+an)=0,又an+1+an>0.
=0,∴[(n+1)an+1﹣nan](an+1+an)=0,又an+1+an>0.
∴(n+1)an+1﹣nan=0,解得 ![]() =
= ![]() .
.
∴an= ![]()
![]() …
… ![]() a1=
a1= ![]()
![]() …
… ![]() ×1=
×1= ![]() .
.
∴an= ![]() .
.
∵数列{bn}的前n项和为Sn且Sn=1﹣bn.
∴n≥2时,bn=Sn﹣Sn﹣1=1﹣bn﹣(1﹣bn﹣1),化为:bn= ![]() bn﹣1.
bn﹣1.
n=1时,b1=S1=1﹣b1,解得b1= ![]() .
.
∴数列{bn}是等比数列,首项与公比都为 ![]() .
.
∴bn= ![]() .
.
(2)解:①cn= ![]() =
= ![]() ,
,
∴数列{cn}的前n项和Tn= ![]() +
+ ![]() +…+
+…+ ![]() .
.
∴ ![]() =
= ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() ,
,
可得: ![]() =
= ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =
=  ﹣
﹣ ![]() ,
,
可得:Sn=2﹣ ![]() .
.
②假设存在正整数m满足m>3,c2,c3,cm成等差数列,
则2c3=c2+cm,
∴ ![]() =
= ![]() +
+ ![]() ,化为:2m﹣2=m.
,化为:2m﹣2=m.
m=4时,满足:2m﹣2=m.
m≥5时,2m﹣2﹣m=(1+1)m﹣2﹣m
=1+ ![]() +
+ ![]() +
+ ![]() +…﹣m
+…﹣m
=1+m﹣2+ ![]() +
+ ![]() +…﹣m
+…﹣m
= ![]() +
+ ![]() +…﹣1>0.
+…﹣1>0.
∴m≥5时,2m﹣2﹣m>0,因此2m﹣2=m无解.
综上只有m=4时,满足m>3,c2,c3,cm成等差数列.
【解析】(1)(n+1)a2n+1+an+1an﹣na ![]() =0,因式分解为[(n+1)an+1﹣nan](an+1+an)=0,又an+1+an>0.可得
=0,因式分解为[(n+1)an+1﹣nan](an+1+an)=0,又an+1+an>0.可得 ![]() =
= ![]() .利用an=
.利用an= ![]()
![]() …
… ![]() a1,可得an.数列{bn}的前n项和为Sn且Sn=1﹣bn.n≥2时,bn=Sn﹣Sn﹣1,化为:bn=
a1,可得an.数列{bn}的前n项和为Sn且Sn=1﹣bn.n≥2时,bn=Sn﹣Sn﹣1,化为:bn= ![]() bn﹣1.n=1时,b1=S1=1﹣b1,解得b1.利用等比数列的通项公式即可得出bn.(2)①cn=
bn﹣1.n=1时,b1=S1=1﹣b1,解得b1.利用等比数列的通项公式即可得出bn.(2)①cn= ![]() =
= ![]() ,利用错位相减法与等比数列的求和公式即可得出.
,利用错位相减法与等比数列的求和公式即可得出.
②假设存在正整数m满足m>3,c2,c3,cm成等差数列,2c3=c2+cm,代入化为:2m﹣2=m.对m分类讨论即可得出.


科目:高中数学 来源: 题型:
【题目】下列函数称为双曲函数:双曲正弦:shx= ![]() ,双曲余弦:chx=
,双曲余弦:chx= ![]() ,双曲正切:thx=
,双曲正切:thx= ![]() .
.
(1)对比三角函数的性质,请你找出它们的三个类似性质;
(2)求双曲正弦shx的导数,并求在点x=0处的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn= ![]() (3n+5),正项等比数列{bn}中,b2=4,b1b7=256.
(3n+5),正项等比数列{bn}中,b2=4,b1b7=256.
(1)求{an}与{bn}的通项公式;
(2)设cn=anbn , 求{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,生产每一吨产品所需的劳动力、煤和电耗如表:
产品品种 | 劳动力(个) | 煤(吨) | 电(千瓦) |
A产品 | 3 | 9 | 4 |
B产品 | 10 | 4 | 5 |
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问该企业如何安排生产,才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinxcos2x,下列结论正确的是( )
A.y=f(x)的图象关于 ![]() 对称
对称
B.y=f(x)的图象关于 ![]() 对称
对称
C.y=f(x)的图象关于y轴对称
D.y=f(x)不是周期函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点. 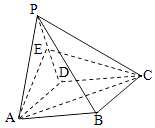
(1)求证:PB⊥AC.
(2)求二面角E﹣AC﹣D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是( )
A.[﹣ ![]() ,
, ![]() ]
]
B.[﹣2,2]
C.[﹣1,1]
D.[﹣4,4]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com