
【题目】某企业生产A,B两种产品,生产每一吨产品所需的劳动力、煤和电耗如表:
产品品种 | 劳动力(个) | 煤(吨) | 电(千瓦) |
A产品 | 3 | 9 | 4 |
B产品 | 10 | 4 | 5 |
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问该企业如何安排生产,才能获得最大利润?
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=2,直线l:y=kx﹣2.
(1)若直线l与圆O交于不同的两点A,B,且 ![]() ,求k的值;
,求k的值;
(2)若 ![]() ,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点分别为C,D,求证:直线CD过定点,并求出该定点的坐标.
,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点分别为C,D,求证:直线CD过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() ,an+1=
,an+1= ![]() (n∈N*).
(n∈N*).
(1)设bn= ![]() ﹣1,证明:数列{bn}是等比数列,并求数列{an}的通项公式an;
﹣1,证明:数列{bn}是等比数列,并求数列{an}的通项公式an;
(2)记数列{nbn}的前n项和为Tn , 求证:Tn<4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,分别根据下列条件解三角形,其中有两解的是( )
A.a=7,b=14,A=30°
B.b=4,c=5,B=30°
C.b=25,c=3,C=150°
D.a= ![]() ,b=
,b= ![]() ,B=60°
,B=60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度). 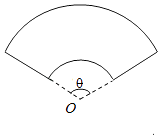
(1)求θ关于x的函数关系式;
(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用之比为y,求y关于x的函数关系式,并求出y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}满足a1=1,(n+1)a2n+1+an+1an﹣na ![]() =0,数列{bn}的前n项和为Sn且Sn=1﹣bn .
=0,数列{bn}的前n项和为Sn且Sn=1﹣bn .
(1)求{an}和{bn}的通项;
(2)令cn= ![]() , ①求{cn}的前n项和Tn;
, ①求{cn}的前n项和Tn;
②是否存在正整数m满足m>3,c2 , c3 , cm成等差数列?若存在,请求出m;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新课标要求学生数学模块学分认定由模块成绩决定,模块成绩由模块考试成绩和平时成绩构成,各占50%,若模块成绩大于或等于60分,获得2学分,否则不能获得学分(为0分),设计一算法,通过考试成绩和平时成绩计算学分,并画出程序框图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com