
【题目】在△ABC中,分别根据下列条件解三角形,其中有两解的是( )
A.a=7,b=14,A=30°
B.b=4,c=5,B=30°
C.b=25,c=3,C=150°
D.a= ![]() ,b=
,b= ![]() ,B=60°
,B=60°
【答案】B
【解析】解:A、∵a=7,b=14,A=30°,
∴由正弦定理得:sinB= ![]() =
= ![]() =1,
=1,
又B为三角形的内角,
∴B=90°,
故只有一解,本选项不合题意;
B、∵b=4,c=5,B=30°,
∴由正弦定理得:sinC= ![]() =
= ![]() =
= ![]() ,
,
又C为三角形的内角,
∴C∈(30°,180°),
可得C有2解,本选项符合题意;
C、∵b=25>c=3,
∴B>C=150°,
∴B+C>300°,矛盾,这样的三角形不存在.
D、∵a= ![]() ,b=
,b= ![]() ,B=60°,
,B=60°,
∴sinA= ![]() =
= ![]() =
= ![]() >1,这样的A不存在,这样的三角形不存在.
>1,这样的A不存在,这样的三角形不存在.
故选:B.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】设a∈R,函数f(x)=|x2﹣2ax|,方程f(x)=ax+a的四个实数解满足x1<x2<x3<x4 .
(1)求a的取值范围;
(2)证明:f(x4)> ![]() +8
+8 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水培植物需要一种植物专用营养液.已知每投放a(1≤a≤4且a∈R)个单位的营养液,它在水中释放的浓度y(克/升)随着时间x(天)变化的函数关系式近似为y=af(x),其中f(x)= 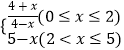 ,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
(1)若只投放一次4个单位的营养液,则有效时间可能达几天?
(2)若先投放2个单位的营养液,3天后投放b个单位的营养液.要使接下来的2天中,营养液能够持续有效,试求b的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知动直线l过点 ![]() ,且与圆O:x2+y2=1交于A、B两点.
,且与圆O:x2+y2=1交于A、B两点. 
(1)若直线l的斜率为 ![]() ,求△OAB的面积;
,求△OAB的面积;
(2)若直线l的斜率为0,点C是圆O上任意一点,求CA2+CB2的取值范围;
(3)是否存在一个定点Q(不同于点P),对于任意不与y轴重合的直线l,都有PQ平分∠AQB,若存在,求出定点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn= ![]() (3n+5),正项等比数列{bn}中,b2=4,b1b7=256.
(3n+5),正项等比数列{bn}中,b2=4,b1b7=256.
(1)求{an}与{bn}的通项公式;
(2)设cn=anbn , 求{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷水的高度,某人在喷水柱正西方向的点A测的水柱顶端的仰角为45°,沿点A向北偏东30°前进100m到达点B.在B点测得水柱顶端的仰角为30°,则水柱的高度是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,生产每一吨产品所需的劳动力、煤和电耗如表:
产品品种 | 劳动力(个) | 煤(吨) | 电(千瓦) |
A产品 | 3 | 9 | 4 |
B产品 | 10 | 4 | 5 |
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问该企业如何安排生产,才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中点. 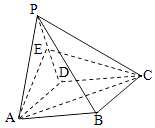
(1)求证:PB⊥AC.
(2)求二面角E﹣AC﹣D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC= ![]() AB=1,M为PB中点.
AB=1,M为PB中点. 
(1)证明:CM∥平面PAD;
(2)求二面角A﹣MC﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com