
����Ŀ��ˮ��ֲ����Ҫһ��ֲ��ר��Ӫ��Һ����֪ÿͶ��a��1��a��4��a��R������λ��Ӫ��Һ������ˮ���ͷŵ�Ũ��y����/��������ʱ��x���죩�仯�ĺ�����ϵʽ����Ϊy=af��x��������f��x��= 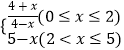 �������Ͷ�ţ���ijһʱ��ˮ�е�Ӫ��ҺŨ��Ϊÿ��Ͷ�ŵ�Ӫ��Һ����Ӧʱ�����ͷŵ�Ũ��֮�ͣ����ݾ��飬��ˮ��Ӫ��Һ��Ũ�Ȳ�����4����/����ʱ����������Ч��
�������Ͷ�ţ���ijһʱ��ˮ�е�Ӫ��ҺŨ��Ϊÿ��Ͷ�ŵ�Ӫ��Һ����Ӧʱ�����ͷŵ�Ũ��֮�ͣ����ݾ��飬��ˮ��Ӫ��Һ��Ũ�Ȳ�����4����/����ʱ����������Ч��
��1����ֻͶ��һ��4����λ��Ӫ��Һ������Чʱ����ܴX�죿
��2������Ͷ��2����λ��Ӫ��Һ��3���Ͷ��b����λ��Ӫ��Һ��Ҫʹ��������2���У�Ӫ��Һ�ܹ�������Ч������b����Сֵ��
���𰸡�
��1���⣺Ӫ��Һ��Ч��������y��4���� 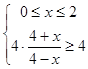 ��
�� 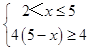 ��
��
��Ϊ0��x��2��2��x��4��
���0��x��4��
����Ӫ��Һ��Чʱ��ɴ�4��
��2���⣺��ڶ���Ͷ��Ӫ��Һ�ij���ʱ��Ϊx�죬
���ʱ��һ��Ͷ��Ӫ��Һ�ij���ʱ��Ϊ��x+3���죬��0��x��2��
��y1Ϊ��һ��Ͷ��Ӫ��Һ��Ũ�ȣ�y2Ϊ�ڶ���Ͷ��Ӫ��Һ��Ũ�ȣ�
yΪˮ�е�Ӫ��Һ��Ũ�ȣ�
��y1=2[5����x+3��]=4��2x��y2=b ![]() ��
��
y=y1+y2=4��2x+b ![]() ��4��[0��2]�Ϻ������
��4��[0��2]�Ϻ������
��b��2x ![]() ��[0��2]�Ϻ����
��[0��2]�Ϻ����
��t=4+x��t��[4��6]����b�ݩ�2��t+ ![]() ��+24��
��+24��
�֩�2��t+ ![]() ��+24��24��22
��+24��24��22 ![]() =24��16
=24��16 ![]() ��
��
���ҽ���t= ![]() ����t=4
����t=4 ![]() ʱ��ȡ�Ⱥţ�
ʱ��ȡ�Ⱥţ�
����b����СֵΪ24��16 ![]() ��
��
��Ҫʹ��������2���У�Ӫ��Һ�ܹ�������Ч��b����СֵΪ24��16 ![]()
����������1��Ӫ��Һ��Ч��������y��4���ɷֶκ�������x���ۣ��ⲻ��ʽ���ɵõ����ۣ���2����ڶ���Ͷ��Ӫ��Һ�ij���ʱ��Ϊx�죬���ʱ��һ��Ͷ��Ӫ��Һ�ij���ʱ��Ϊ��x+3���죬��0��x��2����y1Ϊ��һ��Ͷ��Ӫ��Һ��Ũ�ȣ�y2Ϊ�ڶ���Ͷ��Ӫ��Һ��Ũ�ȣ�yΪˮ�е�Ӫ��Һ��Ũ�ȣ��ɵ�y1=2[5����x+3��]=4��2x��y2=b ![]() ��y=y1+y2=4��2x+b
��y=y1+y2=4��2x+b ![]() ��4��[0��2]�Ϻ���������ò�������ͻ�Ԫ������ϻ�������ʽ�����ɵõ�b����Сֵ��
��4��[0��2]�Ϻ���������ò�������ͻ�Ԫ������ϻ�������ʽ�����ɵõ�b����Сֵ��
�����㾫����������Ŀ����֪���������û�������ʽ����ֵ�����е�Ӧ�õ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ�����û�������ʽ����ֵʱ����������С���Ͷ������Ҫע����������������һ��������������ȡ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
�� ![]() ������
������ ![]() ��
�� ![]() .
.
��1���� ![]() ����СֵΪ-1����ʵ��
����СֵΪ-1����ʵ�� ![]() ��ֵ��
��ֵ��
��2���Ƿ����ʵ�� ![]() ��ʹ����
��ʹ���� ![]() ��
�� ![]() ���ĸ���ͬ����㣿�����ڣ����
���ĸ���ͬ����㣿�����ڣ���� ![]() ��ȡֵ��Χ���������ڣ���˵������.
��ȡֵ��Χ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲO��x2+y2=2��ֱ��l��y=kx��2��
��1����ֱ��l��ԲO���ڲ�ͬ������A��B���� ![]() ����k��ֵ��
����k��ֵ��
��2���� ![]() ��P��ֱ��l�ϵĶ��㣬��P��ԲO����������PC��PD���е�ֱ�ΪC��D����֤��ֱ��CD�����㣬������ö�������꣮
��P��ֱ��l�ϵĶ��㣬��P��ԲO����������PC��PD���е�ֱ�ΪC��D����֤��ֱ��CD�����㣬������ö�������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ�ϵĵ�A��2��3������ֱ��x+2y=0�ĶԳƵ�����Բ�ϣ�����ֱ��x��y+1=0�ཻ���ҳ�Ϊ2 ![]() ����Բ�ķ��̣�
����Բ�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ ![]() �����ҽ���ֱ�ΪF1 �� F2 �� ��F2Ϊ������
�����ҽ���ֱ�ΪF1 �� F2 �� ��F2Ϊ������ ![]() �Ľ��㣬C2����l��C1��Բx2+y2=a2�صõ��ҳ��ֱ�Ϊ
�Ľ��㣬C2����l��C1��Բx2+y2=a2�صõ��ҳ��ֱ�Ϊ ![]() ��4��
��4��
��1����C1��C2�ķ��̣�
��2��ֱ��l1��F1����C2���ཻ��ֱ��l2��F2����l1ƽ�У���l1��C1��A��B��l2��C1����C��D������x���Ϸ������ı���AF1F2C�������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ǡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c����a2=b2+bc���� ![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}����a1= ![]() ��an+1=
��an+1= ![]() ��n��N*����
��n��N*����
��1����bn= ![]() ��1��֤��������{bn}�ǵȱ����У���������{an}��ͨ�ʽan��
��1��֤��������{bn}�ǵȱ����У���������{an}��ͨ�ʽan��
��2��������{nbn}��ǰn���ΪTn �� ��֤��Tn��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У��ֱ�������������������Σ�������������ǣ� ��
A.a=7��b=14��A=30��
B.b=4��c=5��B=30��
C.b=25��c=3��C=150��
D.a= ![]() ��b=
��b= ![]() ��B=60��
��B=60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���¿α�Ҫ��ѧ����ѧģ��ѧ���϶���ģ��ɼ�������ģ��ɼ���ģ�鿼�Գɼ���ƽʱ�ɼ����ɣ���ռ50%����ģ��ɼ����ڻ����60�֣����2ѧ�֣������ܻ��ѧ�֣�Ϊ0�֣������һ�㷨��ͨ�����Գɼ���ƽʱ�ɼ�����ѧ�֣������������ͼ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com