
若命题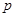 :“
:“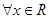 ,都有
,都有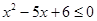 ”,则其
”,则其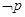 命题为
命题为
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
在整数集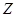 中,被5除所得余数为
中,被5除所得余数为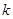 的所有整数组成一个“类”,记为
的所有整数组成一个“类”,记为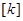 ,即
,即 ,则下列结论正确的为 (写出所有正确的编号)
,则下列结论正确的为 (写出所有正确的编号)
①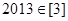 ;
;
②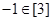 ;
;
③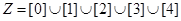 ;
;
④“整数 属于同一类”的充要条件是“
属于同一类”的充要条件是“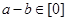 ”;
”;
⑤命题“整数 满足
满足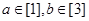 ,则
,则 ”的原命题与逆命题都为真命题.
”的原命题与逆命题都为真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给出下列命题:
①在锐角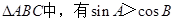 ;
;
②函数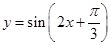 图象关于点
图象关于点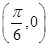 对称;
对称;
③在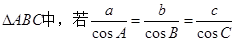 , 则
, 则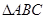 必为等边三角形;
必为等边三角形;
④在同一坐标系中, 函数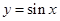 的图象和函数
的图象和函数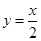 的图象有三个公共点.
的图象有三个公共点.
其中正确命题的序号是______(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列说法中正确的是 .
①“若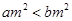 ,则
,则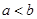 ”的逆命题为真;
”的逆命题为真;
②线性回归方程对应的直线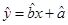 一定经过其样本数据点
一定经过其样本数据点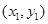 ,
, ,
,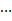 ,
, 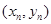 中的一个点;
中的一个点;
③命题“存在实数 ,使得
,使得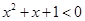 ”的否定是“对任意实数
”的否定是“对任意实数 ,均有
,均有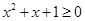 ”
”
④用数学归纳法证明(n+1)(n+2)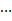 (n+n)=
(n+n)= 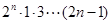 (
(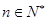 )时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).
)时,从“k”到“k+1”的证明,左边需增添的一个因式是2(2k+1).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列命题正确的是____________.
①若a>b,则alg >blg
>blg ;
;
②若a>b>0,c>d>0,则a2-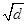 >b2-
>b2-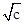 ;
;
③若|a|>b,则a2>b2;
④若a>|b|,则a2>b2.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列若干命题中,正确命题的序号是 。
①“a=3”是直线ax+2y+2a=0和直线3x+(a一l)y一a+7 =0平行的充分不必要条件;
②△ABC中,若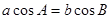 ,则该三角形形状为等腰三角形;
,则该三角形形状为等腰三角形;
③两条异面直线在同一平面内的投影可能是两条互相垂直的直线;
④对于命题 使得
使得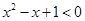 ,则
,则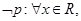 均有
均有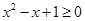 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列叙述正确的序号是 。
(1)对于定义在R上的函数 ,若
,若 ,则函数
,则函数 不是奇函数;
不是奇函数;
(2) 定义在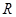 上的函数
上的函数 ,在区间
,在区间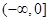 上是单调增函数,在区间
上是单调增函数,在区间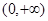 上也是单调增函数,则函数
上也是单调增函数,则函数 在
在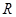 上是单调增函数;
上是单调增函数;
(3) 已知函数的解析式为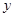 =
=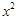 ,它的值域为
,它的值域为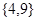 ,那么这样的函数有9个;
,那么这样的函数有9个;
(4)对于任意的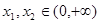 ,若函数
,若函数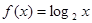 ,则
,则
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com