|
|
|
已知数列{an}的前n项和为Sn,
(1)若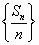 为等差数列,证明{an}为等差数列; 为等差数列,证明{an}为等差数列;
(2)在(1)的条件下,S1=2,S2=6,求数列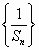 的前n项和Tn; 的前n项和Tn;
(3)在(1)(2)的条件下,若存在实数λ使得对一切n∈N+,有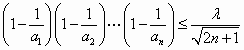 成立,求λ的最小值. 成立,求λ的最小值.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
已知函数f(x)=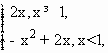 若f(2-a2)<f(a),则实数a的取值范围是 若f(2-a2)<f(a),则实数a的取值范围是
|
| [ ] |
A. |
(-∞,-1)∪(2,+∞)
|
B. |
(-1,2)
|
C. |
(-2,1)
|
D. |
(-∞,-2)∪(1,+∞)
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
设x∈R,则“|x-|>1”是“x>3”的
|
| [ ] |
A. |
充分而不必要条件;
|
B. |
必要而不充分条件;
|
C. |
充分必要条件;
|
D. |
既不充分也不必要条件;
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
咖啡馆配制两种饮料,甲种饮料每杯分别用奶粉、咖啡、糖9 g、4 g、3 g;乙种饮料每杯分别用奶粉、咖啡、糖4 g、5 g、10 g,已知每天使用原料限额为奶粉3600 g,咖啡2000 g,糖3000 g,如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料使用的限额内,饮料能全部售完,问咖啡馆每天怎样安排配制饮料获利最大?
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
已知向量 =(cos =(cos ,sin ,sin ),向量 ),向量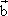 =( =(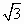 ,-1)则|2 ,-1)则|2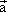 - -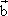 |的最大值,最小值分别是 |的最大值,最小值分别是
|
| [ ] |
A. |
4 ,0 ,0
|
B. |
4,4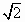
|
C. |
16,0
|
D. |
4,0
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修2
题型:
|
|
|
在平面直角坐标系内,设M(x1,y1)、N(x2,y2)为不同的两点,直线l的方程为ax+by+c=0,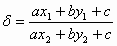 .有四个命题: .有四个命题:
①存在实数△,使点N在直线l上;
②若△=1,则过M、N两点的直线与直线l平行;
③若△=-1,则直线l经过线段MN的中点;
④若△>1,则点M、N在直线l的同侧,且直线l与线段MN的延长线相交.
上述命题中,全部真命题的序号是
|
| [ ] |
A. |
①②③
|
B. |
②③④
|
C. |
①③④
|
D. |
①②③④
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修2
题型:
|
|
|
如图,正四棱锥(底面为正方形,顶点在底面上的射影是底面的中心)S-ABCD的底面边长为4,高为4,E为边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为
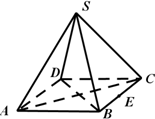
|
| [ ] |
A. |
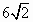
|
B. |
 + +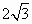
|
C. |
 + +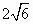
|
D. |
2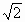
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修3
题型:
|
|
|
小王同学有5本不同的语文书和4本不同的英语书,从中任取2本,则语文书和英语书各有1本的概率为________(结果用分数表示).
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 选修2-1
题型:
|
|
|
已知椭圆的中心是坐标原点O,焦点在x轴上,离心率为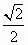 ,又椭圆上任一点到两焦点的距离和为 ,又椭圆上任一点到两焦点的距离和为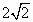 .过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点. .过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
(1)求椭圆的方程;
(2)在线段OF上是否存在点M(m,0),使得|MP|=|MQ|?若存在,求出m的取值范围;若不存在,请说明理由.
|
|
|
查看答案和解析>>

 导学全程练创优训练系列答案
导学全程练创优训练系列答案