|
|
|
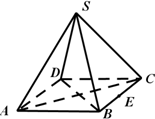
如图,正四棱锥(底面为正方形,顶点在底面上的射影是底面的中心)S-ABCD的底面边长为4,高为4,E为边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为
|
| [ ] |
A. |
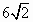
|
B. |
 + +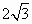
|
C. |
 + +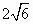
|
D. |
2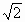
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
sin15°cos15°的值为
|
| [ ] |
A. |
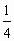
|
B. |
-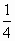
|
C. |
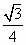
|
D. |
-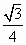
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
已知方程(x2-2x+m)(x2-2x+n)=0的四个实根组成一个首项为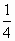 的等差数列,则|m-n|等于 的等差数列,则|m-n|等于
|
| [ ] |
A. |
1
|
B. |
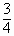
|
C. |
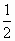
|
D. |
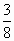
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
已知数列{an}的前n项和为Sn,
(1)若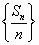 为等差数列,证明{an}为等差数列; 为等差数列,证明{an}为等差数列;
(2)在(1)的条件下,S1=2,S2=6,求数列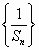 的前n项和Tn; 的前n项和Tn;
(3)在(1)(2)的条件下,若存在实数λ使得对一切n∈N+,有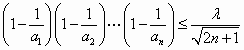 成立,求λ的最小值. 成立,求λ的最小值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修2
题型:
|
|
|
以下说法错误的是
|
| [ ] |
A. |
直角坐标平面内直线的倾斜角的取值范围是[0,π)
|
B. |
直角坐标平面内两条直线夹角的取值范围是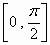
|
C. |
平面内两个非零向量的夹角的取值范围是[0,π)
|
D. |
空间两条直线所成角的取值范围是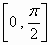
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修2
题型:
|
|
|
若直线y=x+m平分圆x2+y2-4x+2y-2=0的周长,则实数m的值是
|
| [ ] |
A. |
-3
|
B. |
3
|
C. |
-1
|
D. |
1
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修2
题型:
|
|
|
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
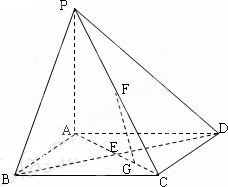
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
(3)当二面角B-PC-D的大小为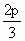 时,求PC与底面ABCD所成角的正切值. 时,求PC与底面ABCD所成角的正切值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修5
题型:
|
|
|
|x|+|y|≤1表示的平面区域的面积是________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 选修4-5 不等式选讲
题型:
|
|
|
选修4-5:不等式选讲
已知函数f(x)=|x-a|.
(Ⅰ)若不等式f(x)≤m的解集为{x|-1≤x≤5},求实数a,m的值;
(Ⅱ)当a=2时,解关于x的不等式f(x)+t≥f(x+2t)(t≥0).
|
|
|
查看答案和解析>>
