|
|
|
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
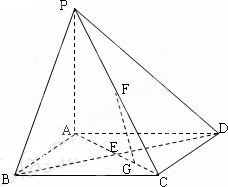
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
(3)当二面角B-PC-D的大小为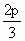 时,求PC与底面ABCD所成角的正切值. 时,求PC与底面ABCD所成角的正切值.
|
|
|
答案:
解析:
|
(1)证明BD⊥平面PAC
(2)当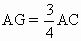 时,FG∥平面PBD 时,FG∥平面PBD
(3)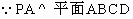 , ,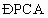 是PC与底面ABCD所成角. 是PC与底面ABCD所成角.
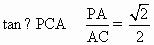
|
练习册系列答案
相关习题
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
已知向量 =(cos =(cos ,sin ,sin ),向量 ),向量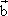 =( =(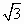 ,-1)则|2 ,-1)则|2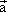 - -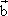 |的最大值,最小值分别是 |的最大值,最小值分别是
|
| [ ] |
A. |
4 ,0 ,0
|
B. |
4,4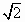
|
C. |
16,0
|
D. |
4,0
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修2
题型:
|
|
|
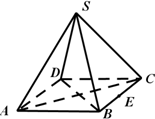
如图,正四棱锥(底面为正方形,顶点在底面上的射影是底面的中心)S-ABCD的底面边长为4,高为4,E为边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为
|
| [ ] |
A. |
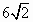
|
B. |
 + +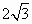
|
C. |
 + +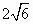
|
D. |
2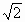
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修2
题型:
|
|
|
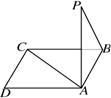
如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是
/A86)
|
| [ ] |
A. |
90°
|
B. |
30°
|
C. |
45°
|
D. |
60°
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修3
题型:
|
|
|
小王同学有5本不同的语文书和4本不同的英语书,从中任取2本,则语文书和英语书各有1本的概率为________(结果用分数表示).
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修5
题型:
|
|
|
在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是
|
| [ ] |
A. |
等腰三角形
|
B. |
直角三角形
|
C. |
等腰直角三角形
|
D. |
等边三角形
|
|
|
查看答案和解析>>
科目:高中数学
来源:苏教版(新课标) 必修1
题型:
|
|
|
对于函数f(x)=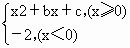 ,有f(4)=f(0),f(1)=-1,则方程f(x)=x的解有 ,有f(4)=f(0),f(1)=-1,则方程f(x)=x的解有
|
| [ ] |
A. |
0个,
|
B. |
1个
|
C. |
2个,
|
D. |
3个.
|
|
|
查看答案和解析>>
