
如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
(1)求此人到达当日空气质量优良的概率;
(2)求此人在该市停留期间只有1天空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
在高中“自选模块”考试中,某考场的每位同学都选了一道数学题,第一小组选《数学史与不等式选讲》的有1人,选《矩阵变换和坐标系与参数方程》的有5人,第二小组选《数学史与不等式选讲》的有2人,选《矩阵变换和坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4人均为选《矩阵变换和坐标系与参数方程》的概率;
(2)设X为选出的4个人中选《数学史与不等式选讲》的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2,现从A、B、C三个箱子中各摸出1个球.
(1) 若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(2) 如果猜测摸出的这三个球的号码之和,猜中有奖,那么猜什么数获奖的可能性最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表中有三个游戏规则,袋子中分别装有大小相同的球,从袋子中取球,分别计算甲获胜的概率,说明哪个游戏是公平的?
| 游戏1 | 游戏2 | 游戏3 |
| 1个红球和1个白球 | 2个红球和2个白球 | 3个红球和1个白球 |
| 取1个球 | 取1个球,再取1个球 | 取1个球,再取1个球 |
| 取出的球是红球→甲胜 | 取出的两个球同色→甲胜 | 取出的两个球同色→甲胜 |
| 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 | 取出的两个球不同色→乙胜 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
第17届亚运会将于2014年9月18日至10月4日在韩国仁川进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱.
(1)根据调查数据制作2×2列联表;
(2)根据列联表的独立性检验,能否认为性别与喜爱运动有关?
| 参考数据 | 当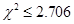 时,无充分证据判定变量 时,无充分证据判定变量 有关联,可以认为两变量无关联; 有关联,可以认为两变量无关联; |
当 时,有 时,有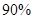 把握判定变量 把握判定变量 有关联; 有关联; | |
当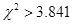 时,有 时,有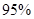 把握判定变量 把握判定变量 有关联; 有关联; | |
当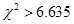 时,有 时,有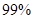 把握判定变量 把握判定变量 有关联. 有关联. |
 ,其中
,其中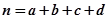 .)
.)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位招聘职工,经过几轮筛选,一轮从2000名报名者中筛选300名进入二轮笔试,接着按笔试成绩择优取100名进入第三轮面试,最后从面试对象中综合考察聘用50名.
(1)求参加笔试的竞聘者能被聘用的概率;
(2)用分层抽样的方式从最终聘用者中抽取10名进行进行调查问卷,其中有3名女职工,求被聘用的女职工的人数;
(3)单位从聘用的三男和二女中,选派两人参加某项培训,至少选派一名女同志参加的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人进行投篮比赛,两人各投3球,谁投进的球数多谁获胜,已知每次投篮甲投进的概率为 ,乙投进的概率为
,乙投进的概率为 ,求:
,求:
(1)甲投进2球且乙投进1球的概率;
(2)在甲第一次投篮未投进的条件下,甲最终获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋内装有6个球,这些球依次被编号为1、2、3、……、6,设编号为n的球重n2-6n+12(单位:克),这些球等可能地从袋里取出(不受重量、编号的影响).
(1)从袋中任意取出一个球,求其重量大于其编号的概率;
(2)如果不放回地任意取出2个球,求它们重量相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球,2个黑球,乙箱子里装有1个白球,2个黑球,这些球除颜色外完全相同.每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖(每次游戏结束后将球放回原箱).
(1)求在1次游戏中:
①摸出3个白球的概率;②获奖的概率.
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com