
求sin210°+cos240°+sin10°cos40°的值.
解法1:因为40°=30°+10°,于是
原式=sin210°+cos2(30°+10°)+sin10°cos(30°+10°)=sin210°+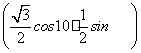 2+sin10°·
2+sin10°·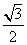 cos10°-
cos10°- sin10°=
sin10°= (sin210°+cos210°)=
(sin210°+cos210°)= .
.
解法2:令sin10°=a+b,cos40°=a-b,则
a= (sin10°+cos40°)=
(sin10°+cos40°)= (sin10°+sin50°)
(sin10°+sin50°)
=sin30°cos20°= cos20°,
cos20°,
b= (sin10°-cos40°)=
(sin10°-cos40°)= (sin10°-sin50°)
(sin10°-sin50°)
=cos30°sin(-20°)=-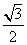 sin20°.
sin20°.
原式=(a+b)2+(a-b)2+(a+b)(a-b)
=3a2+b2
= cos220°+
cos220°+ sin220°=
sin220°= .
.
解法3:设x=sin210°+cos240°+sin10°cos40°,
y=cos210°+sin240°+cos10°sin40°.则
x+y=1+1+sin10°cos40°+cos10°sin40°=2+sin50°=2+cos40°
x-y=cos80°-cos20°- =-sin50°-
=-sin50°-
=-cos40°- ,因此,2x=
,因此,2x=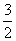 ,x=
,x= .
.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
△ABC中,a、b、c分别为∠A、∠B、∠C的对边,如果a、b、c成等差数列,∠B=30°,△ABC的面积为0.5,那么b为( )
A.1+ B.3+
B.3+
C. 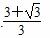 D.2+
D.2+
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com