
【题目】将33![]() 33的方格表中毎个格染三种颜色之一,使得每种颜色的格的个数相等.若相邻两格的颜色不同,则称其公共边为“分隔边".试求分隔边条数的最小值。
33的方格表中毎个格染三种颜色之一,使得每种颜色的格的个数相等.若相邻两格的颜色不同,则称其公共边为“分隔边".试求分隔边条数的最小值。
【答案】56
【解析】
记分隔边的条数为L。首先,将方格表按图分成三个区域,分别染成三种颜色,粗线上均为分隔边。将方格表的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() 。行
。行![]() 中方格出现的颜色数记为
中方格出现的颜色数记为![]() ,列
,列![]() 中方格出现的颜色个数记为
中方格出现的颜色个数记为![]() 。三种颜色分别记为
。三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() 设
设![]() 为含有
为含有![]() 色方格的行数与列数之和。
色方格的行数与列数之和。
定义![]() 类似地定义
类似地定义![]() .计算得到
.计算得到![]()
![]() ,再证明
,再证明![]() ,再证明対任意
,再证明対任意![]() 均有
均有![]() 最后求出分隔边条数的最小值.
最后求出分隔边条数的最小值.
记分隔边的条数为L。首先,将方格表按图分成三个区域,分别染成三种颜色,粗线上均为分隔边。
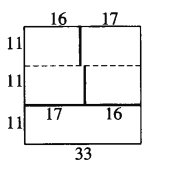
此时,共有56条分隔边,即L=56。
其次证明:L≥56。
将方格表的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() 。行
。行![]() 中方格出现的颜色数记为
中方格出现的颜色数记为![]() ,列
,列![]() 中方格出现的颜色个数记为
中方格出现的颜色个数记为![]() 。三种颜色分别记为
。三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() 设
设![]() 为含有
为含有![]() 色方格的行数与列数之和。
色方格的行数与列数之和。
定义![]()
类似地定义![]() .
.
所以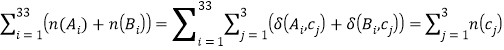
由于染![]() 色的格有
色的格有![]() 个,设含有
个,设含有![]() 色方格的行有a个、列有b个,则
色方格的行有a个、列有b个,则![]() 色的方格一定在这a行和b列的交叉方格中。
色的方格一定在这a行和b列的交叉方格中。
从而,![]()
所以![]() ①
①
由于在行![]() 中有
中有![]() 种颜色的方格,于是,至少有
种颜色的方格,于是,至少有![]() 条分隔边。
条分隔边。
类似地,在列![]() 中,至少有
中,至少有![]() 条分隔边。
条分隔边。
则![]() ②
②
![]() ③
③
下面分两种情形讨论。
1.有一行或一列所有方格同色。
不妨设有一行均为![]() 色则方格表的33列中均含有
色则方格表的33列中均含有![]() 色的方格,又
色的方格,又![]() 色方格有363个,故至少有11行含有
色方格有363个,故至少有11行含有![]() 色方格.于是,
色方格.于是,![]() ④
④
由式①、③、④得
![]()
(2)没有一行也没有一列的所有方格同色.
则対任意![]() 均有
均有
从而,由式②知;
![]()
综上,分割边条数的最小值为56.


科目:高中数学 来源: 题型:
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB![]() EF,矩形ABCD所在平面和圆O所在平面垂直,已知AB=2,EF=1.
EF,矩形ABCD所在平面和圆O所在平面垂直,已知AB=2,EF=1.
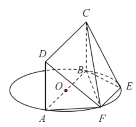
(I)求证:平面DAF⊥平面CBF;
(II)若BC=1,求四棱锥F-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M点为圆心的圆![]() 及其上一点
及其上一点![]() .
.

(1)设圆N与y轴相切,与圆M外切,且圆心在直线![]() 上,求圆N的标准方程;
上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B,C两点且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人.
(i)分别求这5人中经常使用、偶尔或不用共享单车的人数;
(ii)从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过函数![]() 的图象上的两点
的图象上的两点![]() ,
,![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,线段
,线段![]() 与函数
与函数![]() 的图象交于点
的图象交于点![]() ,且
,且![]() 与
与![]() 轴平行.
轴平行.

(1)当![]() ,
,![]() ,
,![]() 时,求实数
时,求实数![]() 的值;
的值;
(2)当![]() 时,求
时,求![]() 的最小值;
的最小值;
(3)已知![]() ,
,![]() ,若
,若![]() ,
,![]() 为区间
为区间![]() 内任意两个变量,且
内任意两个变量,且![]() ,
,
求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出,将冰雪这个冷项目迅速炒“热”.北京某综合大学计划在一年级开设冰球课程,为了解学生对冰球运动的兴趣,随机从该校一年级学生中抽取了100人进行调查,其中女生中对冰球运动有兴趣的占![]() ,而男生有10人表示对冰球运动没有兴趣额.
,而男生有10人表示对冰球运动没有兴趣额.
(1)完成![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“对冰球是否有兴趣与性别有关”?
的把握认为“对冰球是否有兴趣与性别有关”?

(2)若将频率视为概率,现再从该校一年级全体学生中,采用随机抽样的方法每次抽取1名学生,抽取5次,记被抽取的5名学生中对冰球有兴趣的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,期望和方差.
的分布列,期望和方差.
附表:

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生小王自主创业,在乡下承包了一块耕地种植某种水果,每季投入2万元,根据以往的经验,每季收获的此种水果能全部售完,且水果的市场价格和这块地上的产量具有随机性,互不影响,具体情况如表:

(Ⅰ)设![]() 表示在这块地种植此水果一季的利润,求
表示在这块地种植此水果一季的利润,求![]() 的分布列及期望;
的分布列及期望;
(Ⅱ)在销售收入超过5万元的情况下,利润超过5万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温![]() 与该小卖部的这种饮料销量
与该小卖部的这种饮料销量![]() (杯),得到如下数据:
(杯),得到如下数据:
日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)根据(1)中所得的线性回归方程,若天气预报1月16日的白天平均气温![]() ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.
(参考公式: ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com