
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若函数![]() 的值域为
的值域为![]() ,求实数a的取值范围;
,求实数a的取值范围;
(3)设![]() ,若函数
,若函数![]() 有且只有一个零点,求实数a的取值范围.
有且只有一个零点,求实数a的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)利用题意得到对数不等式,求解不等式,即可求得最终结果;
(2)将原问题转化为二次函数的问题,结合二次函数的开口方向和判别式可得关于实数![]() 的不等式组,求解不等式组即可;
的不等式组,求解不等式组即可;
(3)将原问题转化为函数只有一个根的问题,然后分类讨论即可求得最终结果.
(1)当![]() 时,不等式为:
时,不等式为:![]() ,可得:
,可得:![]() ,则不等式解为
,则不等式解为![]() .
.
(2)函数![]() ,
,
设函数![]() 的值域为M,则
的值域为M,则![]() ,
,
当![]() ,即
,即![]() 时,不满足题意,
时,不满足题意,
当![]() ,即
,即![]() 时,
时,![]() ,得实数
,得实数![]() 的取值范围是
的取值范围是![]() .
.
(3)因![]() 有且只有一个零点,
有且只有一个零点,
故![]() ,原问题等价于方程
,原问题等价于方程![]()
当满足![]() 时,只有唯一解,方程(*)化为
时,只有唯一解,方程(*)化为![]() ,
,
①当![]() 时,解得
时,解得![]() ,此时
,此时![]() ,满足题意;
,满足题意;
②当![]() 时,两根均为
时,两根均为![]() ,此时
,此时![]() 也满足;
也满足;
③当![]() 且
且![]() 时,两根为
时,两根为![]() ,
,![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
由题意,![]() ,解得
,解得![]() ,
,
综上,a的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系中,直线l的参数方程为![]() (t为参数,
(t为参数,![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)当![]() 时,写出直线l的普通方程及曲线C的直角坐标方程;
时,写出直线l的普通方程及曲线C的直角坐标方程;
(2)已知点![]() ,设直线l与曲线C交于A,B两点,试确定
,设直线l与曲线C交于A,B两点,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为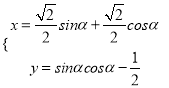 (
(![]() 为参数),若以直角坐标系中的原点为极点,
为参数),若以直角坐标系中的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为实数.)
为实数.)
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理财公司有两种理财产品![]() 和
和![]() ,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]()
投资结果 | 获利20% | 获利10% | 不赔不赚 | 亏损10% |
概率 | 0.2 | 0.3 | 0.2 | 0.3 |
产品![]() (其中
(其中![]() )
)
投资结果 | 获利30% | 不赔不赚 | 亏损20% |
概率 |
| 0.1 |
|
(1)已知甲、乙两人分别选择了产品![]() 和产品
和产品![]() 进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求
进行投资,如果一年后他们中至少有一人获利的概率大于0.7,求![]() 的取值范围;
的取值范围;
(2)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品![]() 和产品
和产品![]() 之中选其一,应选用哪种产品?
之中选其一,应选用哪种产品?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区上年度电价为0.8元![]() ,年用电量为
,年用电量为![]() ,本年度计划将电价降到0.55 元
,本年度计划将电价降到0.55 元![]() 至0.75元
至0.75元![]() 之间,而用户期待电价为0.4元
之间,而用户期待电价为0.4元![]() ,下调电价后新增加的用电量与实际电价和用户期望电价的差成反比(比例系数为K),该地区的电力成本为0.3元
,下调电价后新增加的用电量与实际电价和用户期望电价的差成反比(比例系数为K),该地区的电力成本为0.3元![]() .(注:收益=实际用电量
.(注:收益=实际用电量![]() (实际电价-成本价)),示例:若实际电价为0.6元
(实际电价-成本价)),示例:若实际电价为0.6元![]() ,则下调电价后新增加的用电量为
,则下调电价后新增加的用电量为![]() 元
元![]() )
)
(1)写出本年度电价下调后,电力部门的收益![]() 与实际电价
与实际电价![]() 的函数关系;
的函数关系;
(2)设![]() ,当电价最低为多少仍可保证电力部门的收益比上一年至少增长
,当电价最低为多少仍可保证电力部门的收益比上一年至少增长![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求函数
时,求函数![]() 的最小值
的最小值![]() ;
;
(3)是否存在非负实数![]() ,使得函数
,使得函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com