
若存在过点(1,0)的直线与曲线y=x3和y=ax2+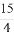 x-9都相切,则a等于( )
x-9都相切,则a等于( )
(A)-1或-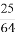 (B)-1或
(B)-1或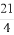
(C)- 或-
或-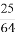 (D)-
(D)- 或7
或7
A
【解析】【思路点拨】先设出切点坐标,再根据导数的几何意义写出切线方程,最后由点(1,0)在切线上求出切点后再求a的值.
解:设过点(1,0)的直线与曲线y=x3相切于点(x0,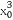 ),所以切线方程为y-
),所以切线方程为y-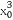 =3
=3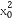 (x-x0),
(x-x0),
即y=3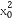 x-2
x-2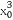 .
.
又(1,0)在切线上,则x0=0或x0=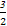 ,
,
当x0=0时,由y=0与y=ax2+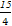 x-9相切可得Δ=(
x-9相切可得Δ=(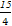 )2-4a(-9)=0,
)2-4a(-9)=0,
解得a=-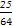 ,
,
同理,当x0=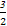 时,由y=
时,由y= x-
x- 与y=ax2+
与y=ax2+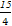 x-9相切可得a=-1,所以选A.
x-9相切可得a=-1,所以选A.
【方法技巧】导数几何意义的应用
导数的几何意义是切点处切线的斜率,应用时主要体现在以下几个方面:
(1)已知切点A(x0,f(x0))求斜率k,即求该点处的导数值:k=f'(x0).
(2)已知斜率k,求切点A(x1,f(x1)),即解方程f'(x1)=k.
(3)已知过某点M(x1,f(x1))(不是切点)的切线斜率为k时,常需设出切点A(x0,f(x0)),利用k= 求解.
求解.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:填空题
里氏震级M的计算公式为:M=lgA-lgA0,其中A是测震仪记录的地震曲线的最大振幅,A0是相应的标准地震的振幅.假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅为0.001,则此次地震的震级为__________级;9级地震的最大振幅是5级地震最大振幅的 倍.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)满足条件f(x+ )+f(x)=0,则ω的值为( )
)+f(x)=0,则ω的值为( )
(A)2π (B)π (C)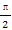 (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十三第二章第十节练习卷(解析版) 题型:解答题
已知曲线y= x3+
x3+ ,
,
(1)求曲线过点P(2,4)的切线方程.
(2)求曲线的斜率为4的切线方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十三第二章第十节练习卷(解析版) 题型:选择题
函数y=cos(2x+1)的导数是( )
(A)y′=sin(2x+1)
(B)y′=-2xsin(2x+1)
(C)y′=-2sin(2x+1)
(D)y′=2xsin(2x+1)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十七第三章第一节练习卷(解析版) 题型:选择题
已知角α的终边上一点的坐标为(sin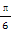 ,cos
,cos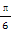 ),则角α的最小正值为( )
),则角α的最小正值为( )
(A)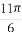 (B)
(B)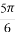 (C)
(C)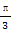 (D)
(D)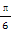
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:选择题
对实数a和b,定义运算“?”:a?b=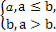 设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
(A)(-∞,-1)∪(- ,0) (B){-1,-
,0) (B){-1,- }
}
(C)(-1,- ) (D)(-∞,-1)∪[-
) (D)(-∞,-1)∪[- ,0)
,0)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十六第十章第三节练习卷(解析版) 题型:选择题
若(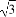 x-
x-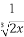 )n的展开式中含有非零常数项,则这样的正整数n的最小值是( )
)n的展开式中含有非零常数项,则这样的正整数n的最小值是( )
(A)3 (B)4 (C)10 (D)12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com