
对实数a和b,定义运算“?”:a?b=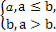 设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
(A)(-∞,-1)∪(- ,0) (B){-1,-
,0) (B){-1,- }
}
(C)(-1,- ) (D)(-∞,-1)∪[-
) (D)(-∞,-1)∪[- ,0)
,0)
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十五第二章第十二节练习卷(解析版) 题型:选择题
函数y=2x3+1的图象与函数y=3x2-b的图象有三个不相同的交点,则实数b的取值范围是( )
(A)(-2,-1) (B)(-1,0)
(C)(0,1) (D)(1,2)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十三第二章第十节练习卷(解析版) 题型:选择题
若存在过点(1,0)的直线与曲线y=x3和y=ax2+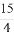 x-9都相切,则a等于( )
x-9都相切,则a等于( )
(A)-1或-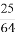 (B)-1或
(B)-1或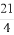
(C)- 或-
或-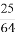 (D)-
(D)- 或7
或7
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十七第三章第一节练习卷(解析版) 题型:选择题
已知扇形的面积为2cm2,扇形圆心角θ的弧度数是4,则扇形的周长为( )
(A)2cm (B)4cm (C)6cm (D)8cm
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:填空题
若函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=1-x2,函数g(x)=lg|x|,则函数y=f(x)与y=g(x)的图象在区间[-5,5]内的交点个数为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:选择题
函数f(x)=|x-2|-lnx在定义域内零点的个数为( )
(A)0 (B)1 (C)2 (D)3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十四第十章第一节练习卷(解析版) 题型:选择题
三张卡片的正反面分别写有1和2,3和4,5和6,若将三张卡片并列,可得到不同的三位数(6不能作9用)的个数为( )
(A)8 (B)6 (C)14 (D)48
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十五第十章第二节练习卷(解析版) 题型:填空题
用数字0,1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有 个(用数字作答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com