
用数字0,1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有 个(用数字作答).
324
【解析】∵个位、十位和百位上的数字之和为偶数,
∴这三个数或者都是偶数,或者有两个奇数一个偶数.
当个位、十位和百位上的都为偶数时,则①此三位中有0,则有 ·4=3×6×4=72(个);②此三位中没有0,则有
·4=3×6×4=72(个);②此三位中没有0,则有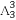 ·3=6×3=18(个).
·3=6×3=18(个).
当个位、十位和百位上有两个奇数一个偶数时,
则①此三位中有0,则有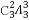 ·4=3×6×4=72(个);②此三位中没有0,则有
·4=3×6×4=72(个);②此三位中没有0,则有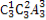 ·3=162(个),∴总共有72+18+72+162=324(个).
·3=162(个),∴总共有72+18+72+162=324(个).
【方法技巧】
1.解决排列组合综合问题,应遵循三大原则:先特殊后一般、先取后排、先分类后分步的原则.
2.解决排列组合综合问题的基本类型
基本类型主要包括:排列中的“在与不在”、组合中的“有与没有”,还有“相邻与不相邻”“至少与至多”“分配与分组”等.
3.解决排列组合综合问题中的转化思想
转化思想就是把一些排列组合问题与基本类型相联系,从而把问题转化为基本类型,然后加以解决.


 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:选择题
对实数a和b,定义运算“?”:a?b=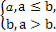 设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
(A)(-∞,-1)∪(- ,0) (B){-1,-
,0) (B){-1,- }
}
(C)(-1,- ) (D)(-∞,-1)∪[-
) (D)(-∞,-1)∪[- ,0)
,0)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十六第十章第三节练习卷(解析版) 题型:选择题
若(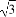 x-
x-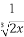 )n的展开式中含有非零常数项,则这样的正整数n的最小值是( )
)n的展开式中含有非零常数项,则这样的正整数n的最小值是( )
(A)3 (B)4 (C)10 (D)12
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十八第十章第五节练习卷(解析版) 题型:选择题
甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中a,b∈{1,2,3,4,5,6},若|a-b|≤1,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十八第十章第五节练习卷(解析版) 题型:选择题
从集合A={-1,1,2}中随机选取一个数记为k,从集合B={-2,1,2}中随机选取一个数记为b,则直线y=kx+b不经过第三象限的概率为( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十五第十章第二节练习卷(解析版) 题型:选择题
两家夫妇各带一个小孩一起到动物园游玩,购票后排队依次入园,为安全起见,首尾一定安排两位爸爸,另外,两个小孩一定排在一起,则这6人的入园顺序排法种数为( )
(A)48 (B)36 (C)24 (D)12
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十五第十章第二节练习卷(解析版) 题型:选择题
如图所示,使电路接通,开关不同的开闭方式有( )

(A)11种 (B)20种
(C)21种 (D)12种
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十二第九章第三节练习卷(解析版) 题型:选择题
10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有( )
(A)a>b>c (B)b>c>a
(C)c>a>b (D)c>b>a
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十一第九章第二节练习卷(解析版) 题型:选择题
某公路设计院有工程师6人,技术员12人,技工18人,要从这些人中抽取n个人参加市里召开的科学技术大会.如果采用系统抽样和分层抽样的方法抽取,不用剔除个体,如果参会人数增加1个,则在采用系统抽样时,需要在总体中先剔除1个个体,则n等于( )
(A)5 (B)6 (C)7 (D)8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com