
某公路设计院有工程师6人,技术员12人,技工18人,要从这些人中抽取n个人参加市里召开的科学技术大会.如果采用系统抽样和分层抽样的方法抽取,不用剔除个体,如果参会人数增加1个,则在采用系统抽样时,需要在总体中先剔除1个个体,则n等于( )
(A)5 (B)6 (C)7 (D)8
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十五第十章第二节练习卷(解析版) 题型:填空题
用数字0,1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有 个(用数字作答).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十九第十章第六节练习卷(解析版) 题型:选择题
在区间(0,1)内任取两个实数,则这两个实数的和大于 的概率为( )
的概率为( )
(A)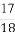 (B)
(B) (C)
(C) (D)
(D)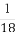
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十七第十章第四节练习卷(解析版) 题型:选择题
在第3,6,16路公共汽车的一个停靠站(假定这个车站只能停靠一辆公共汽车),有一位乘客需在5分钟之内乘上公共汽车赶到厂里,他可乘3路或6路公共汽车到厂里,已知3路公共汽车、6路公共汽车在5分钟之内到此车站的概率分别为0.20和0.60,则该乘客在5分钟内能乘上所需要的车的概率为( )
(A)0.12 (B)0.20 (C)0.60 (D)0.80
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十一第九章第二节练习卷(解析版) 题型:解答题
某单位最近组织了一次健身活动,参加活动的职工分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的 ,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组中不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定
,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组中不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定
(1)游泳组中青年人、中年人、老年人分别所占的比例.
(2)游泳组中青年人、中年人、老年人分别应抽取的人数.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十一第九章第二节练习卷(解析版) 题型:选择题
用系统抽样法从160名学生中抽取容量为20的样本,将160名学生随机地从1~160编号,按编号顺序平均分成20组(1~8号,9~16号,…,153~160号),若第16组抽出的号码为126,则第1组中用抽签的方法确定的号码是( )
(A)5 (B)6 (C)7 (D)8
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十第八章第一节练习卷(解析版) 题型:填空题
若ab>0,且A(a,0),B(0,b),C(-2,-2)三点共线,则ab的最小值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十八第八章第九节练习卷(解析版) 题型:解答题
已知平面内一动点P到点F(1,0)的距离与点P到y轴的距离的差等于1.
(1)求动点P的轨迹C的方程.
(2)过点F作两条斜率存在且互相垂直的直线l1,l2,设l1与轨迹C相交于点A,B,l2与轨迹C相交于点D,E,求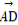 ·
·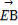 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com