
已知曲线y= x3+
x3+ ,
,
(1)求曲线过点P(2,4)的切线方程.
(2)求曲线的斜率为4的切线方程.
(1) 4x-y-4=0或x-y+2=0 (2) 4x-y-4=0和12x-3y+20=0
【解析】(1)设曲线y=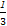 x3+
x3+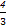 与过点P(2,4)的切线相切于点A(x0,
与过点P(2,4)的切线相切于点A(x0,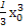 +
+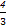 ),则点A处切线的斜率k=
),则点A处切线的斜率k=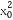 ,∴切线方程为y-(
,∴切线方程为y-(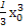 +
+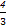 )=
)=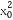 (x-x0),即y=
(x-x0),即y=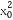 ·x-
·x-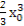 +
+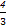 .
.
∵点P(2,4)在切线上,∴4=2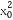 -
-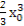 +
+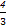 ,即
,即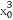 -3
-3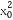 +4=0,∴
+4=0,∴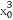 +
+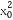 -4
-4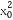 +4=0,
+4=0,
∴(x0+1)(x0-2)2=0,
解得x0=-1或x0=2,
故所求切线的方程为4x-y-4=0或x-y+2=0.
(2)设切点为(x0,y0),
则切线的斜率为k=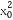 =4,x0=±2,
=4,x0=±2,
所以切点为(2,4),(-2,-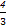 ),
),
∴切线方程为y-4=4(x-2)和y+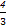 =4(x+2),
=4(x+2),
即4x-y-4=0和12x-3y+20=0.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十六第二章第十三节练习卷(解析版) 题型:选择题
根据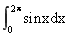 =0推断直线x=0,x=2π,y=0和正弦曲线y=sinx所围成的曲边梯形的面积时,正确结论为( )
=0推断直线x=0,x=2π,y=0和正弦曲线y=sinx所围成的曲边梯形的面积时,正确结论为( )
(A)面积为0
(B)曲边梯形在x轴上方的面积大于在x轴下方的面积
(C)曲边梯形在x轴上方的面积小于在x轴下方的面积
(D)曲边梯形在x轴上方的面积等于在x轴下方的面积
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:解答题
为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,新上了把二氧化碳处理转化为一种可利用的化工产品的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为
y=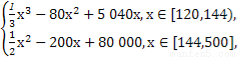
且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
函数y=2sin(2x+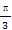 )的图象关于点P(x0,0)对称,若x0∈[-
)的图象关于点P(x0,0)对称,若x0∈[-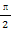 ,0],则x0等于( )
,0],则x0等于( )
(A)-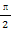 (B)-
(B)-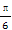 (C)-
(C)- (D)-
(D)-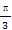
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
函数y=- cos2x+
cos2x+ 的递增区间是( )
的递增区间是( )
(A)(kπ,kπ+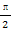 )(k∈Z)
)(k∈Z)
(B)(kπ+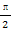 ,kπ+π)(k∈Z)
,kπ+π)(k∈Z)
(C)(2kπ,2kπ+π)(k∈Z)
(D)(2kπ+π,2kπ+2π)(k∈Z)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十三第二章第十节练习卷(解析版) 题型:选择题
若存在过点(1,0)的直线与曲线y=x3和y=ax2+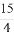 x-9都相切,则a等于( )
x-9都相切,则a等于( )
(A)-1或-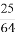 (B)-1或
(B)-1或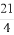
(C)- 或-
或-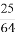 (D)-
(D)- 或7
或7
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十七第三章第一节练习卷(解析版) 题型:解答题
已知角α终边经过点P(x,-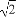 )(x≠0),且cosα=
)(x≠0),且cosα=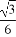 x.求sinα+
x.求sinα+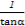 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:填空题
若函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=1-x2,函数g(x)=lg|x|,则函数y=f(x)与y=g(x)的图象在区间[-5,5]内的交点个数为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十六第十章第三节练习卷(解析版) 题型:填空题
已知(1+x)+(1+x)2+…+(1+x)n=a0+a1x+a2x2+…+anxn,且a1+a2+…+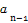 =29-n,则n= .
=29-n,则n= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com