
为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,新上了把二氧化碳处理转化为一种可利用的化工产品的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为
y=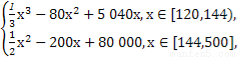
且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(1) 国家每月至少补贴5000元才能使该项目不亏损
(2) 当每月的处理量为400吨时,才能使每吨的平均处理成本最低.
【解析】(1)该项目不会获利.
当x∈[200,300]时,设该项目获利为S,
则S=200x-(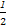 x2-200x+80000)
x2-200x+80000)
=-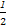 x2+400x-80000=-
x2+400x-80000=-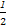 (x-400)2,
(x-400)2,
所以当x∈[200,300]时,S<0,因此该项目不会获利.
当x=300时,S取得最大值-5000,
所以国家每月至少补贴5000元才能使该项目不亏损.
(2)由题意,可知二氧化碳的每吨处理成本为:
 =
=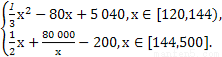
①当x∈[120,144)时,
 =
=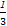 x2-80x+5040=
x2-80x+5040=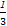 (x-120)2+240,
(x-120)2+240,
所以当x=120时, 取得最小值240.
取得最小值240.
②当x∈[144,500]时, =
=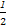 x+
x+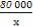 -200≥
-200≥
2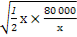 -200=200,
-200=200,
当且仅当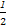 x=
x=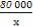 ,
,
即x=400时, 取得最小值200.
取得最小值200.
因为200<240,所以当每月的处理量为400吨时,才能使每吨的平均处理成本最低.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十第二章第七节练习卷(解析版) 题型:填空题
已知函数f(x)=|x+1|+|x-a|的图象关于直线x=1对称,则a的值是_________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十八第三章第二节练习卷(解析版) 题型:填空题
设f(x)=sinx+cosx,f′(x)是f(x)的导数,若f(x)=2f′(x),则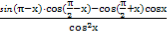 =_________.
=_________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十五第二章第十二节练习卷(解析版) 题型:解答题
已知两函数f(x)=8x2+16x-k,g(x)=2x3+5x2+4x,其中k为实数.
(1)对任意x∈[-3,3]都有f(x)≤g(x)成立,求k的取值范围.
(2)存在x∈[-3,3]使f(x)≤g(x)成立,求k的取值范围.
(3)对任意x1,x2∈[-3,3]都有f(x1)≤g(x2),求k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十五第二章第十二节练习卷(解析版) 题型:选择题
在半径为R的半球内有一内接圆柱,则这个圆柱的体积的最大值是( )
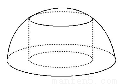
(A)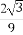 πR3 (B)
πR3 (B)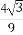 πR3
πR3
(C)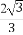 πR3 (D)
πR3 (D) πR3
πR3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:填空题
里氏震级M的计算公式为:M=lgA-lgA0,其中A是测震仪记录的地震曲线的最大振幅,A0是相应的标准地震的振幅.假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅为0.001,则此次地震的震级为__________级;9级地震的最大振幅是5级地震最大振幅的 倍.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:填空题
关于函数f(x)=4sin(2x+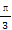 )(x∈R),有下列命题:
)(x∈R),有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是π的整数倍;
②y=f(x)的表达式可改写为y=4 cos(2x-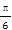 );
);
③y=f(x)的图象关于点(-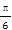 ,0)对称;
,0)对称;
④y=f(x)的图象关于直线x=-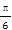 对称.
对称.
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十三第二章第十节练习卷(解析版) 题型:解答题
已知曲线y= x3+
x3+ ,
,
(1)求曲线过点P(2,4)的切线方程.
(2)求曲线的斜率为4的切线方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:选择题
若x0是函数f(x)=( )x-
)x-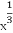 的零点,则x0属于区间( )
的零点,则x0属于区间( )
(A)(-1,0) (B)(0,1)
(C)(1,2) (D)(2,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com