
关于函数f(x)=4sin(2x+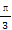 )(x∈R),有下列命题:
)(x∈R),有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是π的整数倍;
②y=f(x)的表达式可改写为y=4 cos(2x-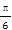 );
);
③y=f(x)的图象关于点(-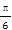 ,0)对称;
,0)对称;
④y=f(x)的图象关于直线x=-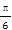 对称.
对称.
其中正确命题的序号是 .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:解答题
设f(x)=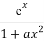 ,其中a为正实数.
,其中a为正实数.
(1)当a= 时,求f(x)的极值点.
时,求f(x)的极值点.
(2)若f(x)为[ ,
, ]上的单调函数,求a的取值范围.
]上的单调函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十八第三章第二节练习卷(解析版) 题型:选择题
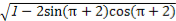 等于( )
等于( )
(A)sin2-cos2 (B)cos2-sin2
(C)±(sin2-cos2) (D)sin2+cos2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:解答题
为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,新上了把二氧化碳处理转化为一种可利用的化工产品的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为
y=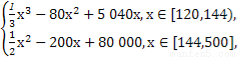
且每处理一吨二氧化碳得到可利用的化工产品价值为200元,若该项目不获利,国家将给予补偿.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:选择题
在某个物理实验中,测得变量x和变量y的几组数据,如下表:
x | 0.50 | 0.99 | 2.01 | 3.98 |
y | -0.99 | 0.01 | 0.98 | 2.00 |
则对x,y最适合的拟合函数是( )
(A)y=2x (B)y=x2-1
(C)y=2x-2 (D)y=log2x
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
函数y=2sin(2x+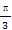 )的图象关于点P(x0,0)对称,若x0∈[-
)的图象关于点P(x0,0)对称,若x0∈[-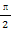 ,0],则x0等于( )
,0],则x0等于( )
(A)-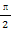 (B)-
(B)-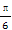 (C)-
(C)- (D)-
(D)-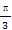
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
函数y=- cos2x+
cos2x+ 的递增区间是( )
的递增区间是( )
(A)(kπ,kπ+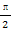 )(k∈Z)
)(k∈Z)
(B)(kπ+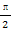 ,kπ+π)(k∈Z)
,kπ+π)(k∈Z)
(C)(2kπ,2kπ+π)(k∈Z)
(D)(2kπ+π,2kπ+2π)(k∈Z)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十七第三章第一节练习卷(解析版) 题型:解答题
已知角α终边经过点P(x,-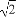 )(x≠0),且cosα=
)(x≠0),且cosα=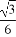 x.求sinα+
x.求sinα+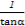 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十四第十章第一节练习卷(解析版) 题型:解答题
某城市在中心广场建造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有多少种(用数字作答).
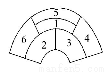
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com