
设f(x)=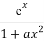 ,其中a为正实数.
,其中a为正实数.
(1)当a= 时,求f(x)的极值点.
时,求f(x)的极值点.
(2)若f(x)为[ ,
, ]上的单调函数,求a的取值范围.
]上的单调函数,求a的取值范围.
(1) x1=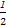 是极大值点,x2=
是极大值点,x2=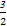 是极小值点 (2) 0<a≤1或a≥
是极小值点 (2) 0<a≤1或a≥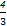
【解析】f'(x)=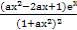 .
.
(1)当a=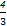 时,若f'(x)=0,则4x2-8x+3=0
时,若f'(x)=0,则4x2-8x+3=0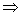 x1=
x1=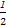 ,x2=
,x2=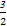 ,则
,则
x | (-∞, |
| ( |
| ( |
f'(x) | + | 0 | - | 0 | + |
f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
∴x1=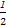 是极大值点,x2=
是极大值点,x2=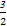 是极小值点.
是极小值点.
(2)记g(x)=ax2-2ax+1,则
g(x)=a(x-1)2+1-a,
∵f(x)为[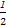 ,
,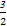 ]上的单调函数,
]上的单调函数,
则f'(x)在[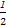 ,
,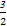 ]上不变号,
]上不变号,
∵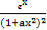 >0,
>0,
∴g(x)≥0或g(x)≤0对x∈[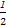 ,
,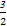 ]恒成立,
]恒成立,
又g(x)的对称轴为x=1,故g(x)的最小值为g(1),最大值为g(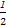 ).
).
由g(1)≥0或g(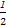 )≤0
)≤0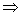 0<a≤1或a≥
0<a≤1或a≥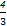 ,
,
∴a的取值范围是0<a≤1或a≥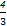 .
.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:选择题
侧面都是直角三角形的正三棱锥,底面边长为a时,该三棱锥的全面积是( )
(A) a2 (B)
a2 (B) a2
a2
(C) a2 (D)
a2 (D) a2
a2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:选择题
在用数学归纳法证明凸n边形内角和定理时,第一步应验证( )
(A)n=1时成立 (B)n=2时成立
(C)n=3时成立 (D)n=4时成立
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十第二章第七节练习卷(解析版) 题型:填空题
已知函数f(x)=|x+1|+|x-a|的图象关于直线x=1对称,则a的值是_________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:选择题
函数y=f′(x)是函数y=f(x)的导函数,且函数y=f(x)在点P(x0,f(x0))处的切线为l:y=g(x)=f′(x0)·(x-x0)+f(x0),F(x)=f(x)-g(x), 如果函数y=f(x)在区间[a,b]上的图象如图所示,且a<x0<b,那么( )
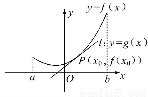
(A)F'(x0)=0,x=x0是F(x)的极大值点
(B)F'(x0)=0,x=x0是F(x)的极小值点
(C)F'(x0)≠0,x=x0不是F(x)的极值点
(D)F'(x0)≠0,x=x0是F(x)的极值点
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十六第二章第十三节练习卷(解析版) 题型:解答题
求由抛物线y2=x-1与其在点(2,1),(2,-1)处的切线所围成的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十八第三章第二节练习卷(解析版) 题型:填空题
设f(x)=sinx+cosx,f′(x)是f(x)的导数,若f(x)=2f′(x),则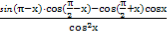 =_________.
=_________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:填空题
关于函数f(x)=4sin(2x+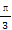 )(x∈R),有下列命题:
)(x∈R),有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是π的整数倍;
②y=f(x)的表达式可改写为y=4 cos(2x-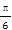 );
);
③y=f(x)的图象关于点(-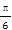 ,0)对称;
,0)对称;
④y=f(x)的图象关于直线x=-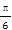 对称.
对称.
其中正确命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com