
 =(1,cosx),
=(1,cosx),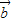 =(
=( ,-sinx)
,-sinx)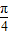 ]时,若
]时,若 ,求x的值;
,求x的值;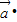
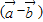 ,x∈R,求f(x)的最小正周期及最大值.
,x∈R,求f(x)的最小正周期及最大值.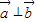 ,则
,则 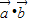 =0,求得sin2x 的值,根据2x的范围,求出2x的值,即得x的值.
=0,求得sin2x 的值,根据2x的范围,求出2x的值,即得x的值. +
+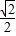 sin(2x+
sin(2x+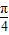 ),则 T=π,最大值为
),则 T=π,最大值为 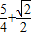 ,此时 x=kπ+
,此时 x=kπ+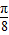 ,k∈z.
,k∈z.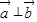 ,则
,则 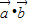 =
= -sinxcosx=0,∴sin2x=
-sinxcosx=0,∴sin2x= ,∵x∈[0,
,∵x∈[0,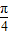 ],
],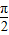 ],∴2x=
],∴2x=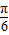 ,x=
,x=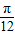 .
.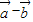 =(
=( ,cosx+sinx ),∴f(x)=
,cosx+sinx ),∴f(x)= +cosx (cosx+sinx )=
+cosx (cosx+sinx )= +
+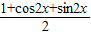
 +
+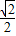 sin(2x+
sin(2x+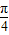 ),
),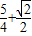 ,此时 x=kπ+
,此时 x=kπ+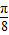 ,k∈z.
,k∈z.

科目:高中数学 来源: 题型:
| AB |
| MB |
| BC |
| OM |
| CO |
| AB |
| a |
| b |
| e1 |
| e2 |
| 1 |
| 2 |
| 3 |
| 4 |
| a |
| b |
| a |
| b |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| α |
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| AP |
| AO |
| AC |
| PA |
| PB |
| PC |
查看答案和解析>>
科目:高中数学 来源:2002年高中会考数学必备一本全2002年1月第1版 题型:044
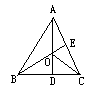
如图,已知△ABC的高AD、BE交于O点,连接CO.(1)用AC、BC、BO所示向量表示AO所示向量;(2)用向量证明:CO⊥A B.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| AB |
| MB |
| BC |
| OM |
| CO |
| AB |
| a |
| b |
| e1 |
| e2 |
| 1 |
| 2 |
| 3 |
| 4 |
| a |
| b |
| a |
| b |
| a |
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com