
【题目】已知某企业有职工5000人,其中男职工3500人,女职工1500人.该企业为了丰富职工的业余生活,决定新建职工活动中心,为此,该企业工会采用分层抽样的方法,随机抽取了300名职工每周的平均运动时间(单位:h),汇总得到频率分布表(如表所示),并据此来估计该企业职工每周的运动时间:
平均运动时间 | 频数 | 频率 |
[0,2) | 15 | 0.05 |
[2,4) | m | 0.2 |
[4,6) | 45 | 0.15 |
[6,8) | 755 | 0.25 |
[8,10) | 90 | 0.3 |
[10,12) | p | n |
合计 | 300 | 1 |
(1)求抽取的女职工的人数;
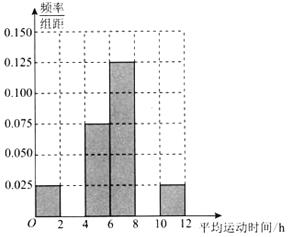
(2)①根据频率分布表,求出m、n、p的值,完成如图所示的频率分布直方图,并估计该企业职工每周的平均运动时间不低于4h的概率;
男职工 | 女职工 | 总计 | |
平均运动时间低于4h | |||
平均运动时间不低于4h | |||
总计 |
②若在样本数据中,有60名女职工每周的平均运动时间不低于4h,请完成以下2×2列联表,并判断是否有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h与性别有关”.
附:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【答案】(1)90;(2)①![]() ,见解析②有
,见解析②有![]() 以上的把握认为“该企业职工毎周的平均运动时间不低于
以上的把握认为“该企业职工毎周的平均运动时间不低于![]() 与性别有关”.
与性别有关”.
【解析】
(1)直接由分层抽样中每层所占比例相等求得抽取的女职工的人数;(2)①由图表数据及频率和为1求得n,然后依次求p与m的值,并完成频率分布直方图;②填写2×2列联表,再由公式求得K2,则结论可求.
(1)抽取的女职工的人数为![]() ;
;
(2)①![]() ,
,
![]() ,
,![]() ;
;
直方图如图:
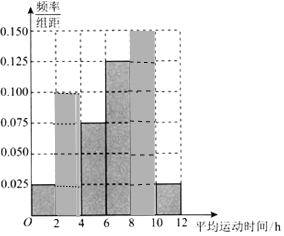
估计该企业职工每周的平均运动时间不低于![]() 的概率为:
的概率为:![]() ;
;
②![]() 列联表如图:
列联表如图:
男职工 | 女职工 | 总计 | |
平均运动时间低于 | 45 | 30 | 75 |
平均运动时间不低于 | 165 | 60 | 225 |
总计 | 210 | 90 | 300 |
![]()
![]() .
.
∴有![]() 以上的把握认为“该企业职工毎周的平均运动时间不低于
以上的把握认为“该企业职工毎周的平均运动时间不低于![]() 与性别有关”.
与性别有关”.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4
的两个焦点与短轴的一个端点是等边三角形的三个顶点,且长轴长为4
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 是椭圆
是椭圆![]() 的左顶点,经过左焦点
的左顶点,经过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 与
与![]() 的面积之差的绝对值的最大值,并求取得最大值时直线
的面积之差的绝对值的最大值,并求取得最大值时直线![]() 的方程.
的方程.![]() 为坐标原点)
为坐标原点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() 离心率
离心率![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)经过椭圆左焦点![]() 的直线(不经过点
的直线(不经过点![]() 且不与
且不与![]() 轴重合)与椭圆交于
轴重合)与椭圆交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .则是否存在常数
.则是否存在常数![]() ,使得向量
,使得向量![]()
![]() 共线?若存在求出
共线?若存在求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面ABCD是边长为3的正方形,EFG分别是棱ABPBPC的中点,
,底面ABCD是边长为3的正方形,EFG分别是棱ABPBPC的中点,![]() ,
,![]() .
.

(Ⅰ)求证:平面EFG∥平面PAD;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() 有一个公共点.
有一个公共点.
(1)求抛物线方程;
(2)斜率不为0的直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,交抛物线于两点
,交抛物线于两点![]() ,
,![]() .抛物线
.抛物线![]() 上是否存在两点
上是否存在两点![]() ,
,![]() 关于直线
关于直线![]() 对称?若存在,求出
对称?若存在,求出![]() 的斜率的取值范围;若不存在,请说明理由.
的斜率的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电力公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行综合排序,综合排序高者中标.
分值权重表如下:
总分 | 技术 | 商务 | 报价 |
100% | 50% | 10% | 40% |
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的.报价表则相对灵活,报价标的评分方法是:基准价的基准分是68分,若报价每高于基准价1%,则在基准分的基础上扣0.8分,最低得分48分;若报价每低于基准价1%,则在基准分的基础上加0.8分,最高得分为80分.若报价低于基准价15%以上(不含15%)每再低1%,在80分在基础上扣0.8分.
在某次招标中,若基准价为1000(万元).甲、乙两公司综合得分如下表:
公司 | 技术 | 商务 | 报价 |
甲 | 80分 | 90分 | A甲分 |
乙 | 70分 | 100分 | A乙分 |
甲公司报价为1100(万元),乙公司的报价为800(万元)则甲,乙公司的综合得分,分别是( )
A. 73,75.4B. 73,80C. 74.6,76D. 74.6,75.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知cos2B+cosB=1-cosAcosC.
(1)求证:a,b,c成等比数列;
(2)若b=2,求△ABC的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() 垂直
垂直![]() 交
交![]() 于
于![]() ,如图①.将
,如图①.将![]() 沿
沿![]() 折起,使
折起,使![]() 到达
到达![]() 的位置,且使平面
的位置,且使平面![]() 平面
平面![]() ,连接
,连接![]() ,
,![]() ,如图②.
,如图②.
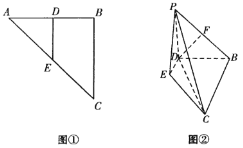
(Ⅰ)若![]() 为
为![]() 的中点,
的中点,![]() ,求证:
,求证:![]() ;
;
(Ⅱ)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列![]() 中,
中,![]() ,
,![]() .令
.令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)是否存在正整数![]() ,(
,(![]()
![]() ),使得
),使得![]() ,
,![]() ,
,![]() 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的![]() ,
,![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com