
【题目】等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() 垂直
垂直![]() 交
交![]() 于
于![]() ,如图①.将
,如图①.将![]() 沿
沿![]() 折起,使
折起,使![]() 到达
到达![]() 的位置,且使平面
的位置,且使平面![]() 平面
平面![]() ,连接
,连接![]() ,
,![]() ,如图②.
,如图②.
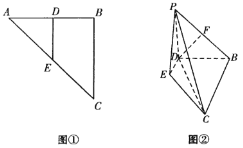
(Ⅰ)若![]() 为
为![]() 的中点,
的中点,![]() ,求证:
,求证:![]() ;
;
(Ⅱ)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的余弦值.
的余弦值.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,从流水线上随机抽取100件产品,统计其质量指标值并绘制频率分布直方图(如图):
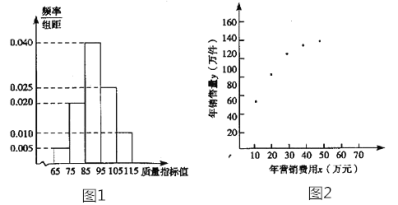
规定产品的质量指标值在![]() 的为劣质品,在
的为劣质品,在![]() 的为优等品,在
的为优等品,在![]() 的为特优品,销售时劣质品每件亏损1元,优等品每件盈利3元,特优品每件盈利5元.以这100 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
的为特优品,销售时劣质品每件亏损1元,优等品每件盈利3元,特优品每件盈利5元.以这100 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
(1)求每件产品的平均销售利润;
(2)该企业为了解年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对近5年年营销费用
(单位:万件)的影响,对近5年年营销费用![]() 和年销售量
和年销售量![]() 数据做了初步处理,得到如图的散点图及一些统计量的值.
数据做了初步处理,得到如图的散点图及一些统计量的值.
|
|
|
|
16.30 | 23.20 | 0.81 | 1.62 |
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
①求![]() 关于
关于![]() 的回归方程;
的回归方程;
⑦用所求的回归方程估计该企业应投人多少年营销费,才能使得该企业的年收益的预报值达到最大?(收益=销售利润营销费用,取![]() )
)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() 其回归直线
其回归直线![]() 均斜率和截距的最小二乘估计分别为
均斜率和截距的最小二乘估计分别为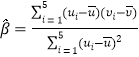 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
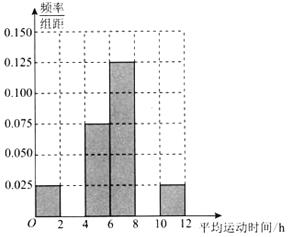
【题目】已知某企业有职工5000人,其中男职工3500人,女职工1500人.该企业为了丰富职工的业余生活,决定新建职工活动中心,为此,该企业工会采用分层抽样的方法,随机抽取了300名职工每周的平均运动时间(单位:h),汇总得到频率分布表(如表所示),并据此来估计该企业职工每周的运动时间:
平均运动时间 | 频数 | 频率 |
[0,2) | 15 | 0.05 |
[2,4) | m | 0.2 |
[4,6) | 45 | 0.15 |
[6,8) | 755 | 0.25 |
[8,10) | 90 | 0.3 |
[10,12) | p | n |
合计 | 300 | 1 |
(1)求抽取的女职工的人数;
(2)①根据频率分布表,求出m、n、p的值,完成如图所示的频率分布直方图,并估计该企业职工每周的平均运动时间不低于4h的概率;
男职工 | 女职工 | 总计 | |
平均运动时间低于4h | |||
平均运动时间不低于4h | |||
总计 |
②若在样本数据中,有60名女职工每周的平均运动时间不低于4h,请完成以下2×2列联表,并判断是否有95%以上的把握认为“该企业职工毎周的平均运动时间不低于4h与性别有关”.
附:K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,过
,过![]() 点作
点作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,
,![]() .连结
.连结![]() ,交
,交![]() 于点
于点![]() ,如图1,将
,如图1,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.
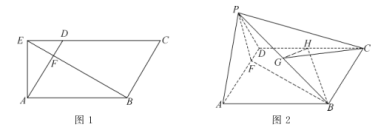
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 经过点
经过点![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,
,![]() ,
,![]() 点在椭圆上,且满足
点在椭圆上,且满足![]() 的
的![]() 点只有两个.
点只有两个.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 且不垂直于坐标轴的直线
且不垂直于坐标轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,在
两点,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的角平分线是
的角平分线是![]() 轴?若存在求出
轴?若存在求出![]() ,若不存在,说明理由.
,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,在圆
,在圆![]() :
:![]() 上任取一点
上任取一点![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .(如图).
.(如图).

(1)求点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)若过点![]() 的动直线
的动直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 相交于
相交于![]() 、
、![]() 两点.问:平面内是否存在异于点
两点.问:平面内是否存在异于点![]() 的定点
的定点![]() ,使得
,使得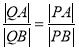 恒成立?试证明你的结论.
恒成立?试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)已知动直线![]() 与圆
与圆![]() :
:![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点.是否存在实数
两点.是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() 是由直线
是由直线![]() 引出的三个不重合的半平面,其中二面角
引出的三个不重合的半平面,其中二面角![]() 大小为60°,
大小为60°,![]() 在二面角
在二面角![]() 内绕直线
内绕直线![]() 旋转,圆
旋转,圆![]() 在
在![]() 内,且圆
内,且圆![]() 在
在![]() ,
,![]() 内的射影分别为椭圆
内的射影分别为椭圆![]() ,
,![]() .记椭圆
.记椭圆![]() ,
,![]() 的离心率分别为
的离心率分别为![]() ,
,![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
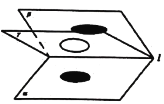
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过两点A(0,4),B(4,6),且圆心在直线x﹣2y﹣2=0上.
(1)求圆C的方程;
(2)若直线l过原点且被圆C截得的弦长为6,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com