
分析 (Ⅰ)求出原函数的导函数,然后对a分类分析,a≥0时,f'(x)>0恒成立,此时f(x)在R上单调递增,无极值;当a<0时,由分别由f'(x)>0和f'(x)<0求得x的取值范围,得到原函数的单调区间并求得极值;
(Ⅱ)令g(x)=f(x)-x2+3=2ex-(x-a)2+3,x≥0,求其导函数,由导函数的导数恒大于等于0可得导函数单调递增,然后对a分类分析求解实数a的取值范围.
解答 解:(Ⅰ)f'(x)=2ex+2a,
①a≥0时,f'(x)>0恒成立,此时f(x)在R上单调递增,无极值;
②当a<0时,由f'(x)>0,得x>ln(-a);
由f'(x)<0,得x<ln(-a),此时f(x)在(-∞,ln(-a))上递减,在[ln(-a),+∞)上递增.
在x=ln(-a)处取得极小值,f(x)极小=f(ln(-a))=2aln(-a)-2a-a2 .
综上可得:a≥0时,单调递增区间为(-∞,+∞),无极值;a<0时,单调递减区间为(-∞,ln(-a)),
递增区间为[ln(-a),+∞),在x=ln(-a)处取得极小值,f(x)极小=f(ln(-a))=2aln(-a)-2a-a2,无极大值.
(Ⅱ)令g(x)=f(x)-x2+3=2ex-(x-a)2+3,x≥0,
则g′(x)=2(ex-x+a),
又令h(x)=2(ex-x+a),则h′(x)=2(ex-1)≥0,
∴h(x)在[0,+∞)上递增,且h(0)=2(a+1).
①当a≥-1时,g′(x)≥0恒成立,即函数g(x)在[0,+∞)上递增,
从而须满足g(0)=5-a2≥0,解得$-\sqrt{5}≤a≤\sqrt{5}$,
又a≥-1,∴$-1≤a≤\sqrt{5}$;
②当a<-1时,则?x0>0,使h(x0)=0,且x∈(0,x0)时,h(x)<0,
即g′(x)<0,即g(x)递减,x∈(x0,+∞)时,h(x)>0,即g'(x)>0,即g(x)递增.
∴$g(x)_{min}=g({x}_{0})=2{e}^{{x}_{0}}-({x}_{0}-a)^{2}+3≥0$,又$h({x}_{0})=2({e}^{{x}_{0}}-{x}_{0}+a)=0$,
从而$2{e}^{{x}_{0}}-({e}^{{x}_{0}})^{2}+3≥0$,解得0<x0≤ln3,
由${e}^{{x}_{0}}={x}_{0}-a$⇒$a={x}_{0}-{e}^{{x}_{0}}$,
令M(x)=x-ex,0<x≤ln3,
则M′(x)=1-ex<0,
∴M(x)在(0,ln3]上递减,
则M(x)≥M(ln3)=ln3-3,又M(x)<M(0)=-1,
故 ln3-3≤a<-1,
综上ln3-3≤a≤5.
点评 本题考查利用导数研究函数的单调性,考查利用导数求函数的最值,体现了分类讨论的数学思想方法和数学转化思想方法,是压轴题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,E,F分别是BC,PC的中点,H是PD上的动点,EH与平面PAD所成的角为θ.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,E,F分别是BC,PC的中点,H是PD上的动点,EH与平面PAD所成的角为θ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
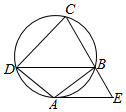 如图,在圆内接梯形ABCD中,AB∥CD.过点A作圆的切线与CB的延长线交于点E,若AB=AD=3,BE=2,
如图,在圆内接梯形ABCD中,AB∥CD.过点A作圆的切线与CB的延长线交于点E,若AB=AD=3,BE=2,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com