
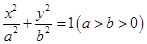 的左右两焦点分别为
的左右两焦点分别为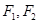 ,
,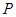 是椭圆上一点,且在
是椭圆上一点,且在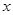 轴上方,
轴上方,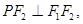
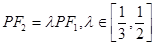 .
.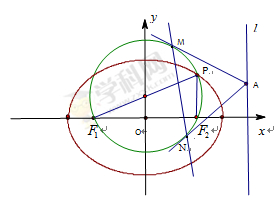
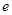 的取值范围;
的取值范围;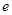 取最大值时,过
取最大值时,过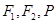 的圆
的圆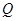 的截
的截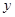 轴的线段长为6,求椭圆的方程;
轴的线段长为6,求椭圆的方程;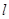 上任一点
上任一点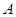 引圆
引圆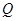 的两条切线,切点分别为
的两条切线,切点分别为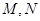 .试探究直线
.试探究直线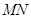 是否过定点?若过定点,请求出该定点;否则,请说明理由.
是否过定点?若过定点,请求出该定点;否则,请说明理由. ;(2)
;(2)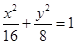 ;(3)
;(3)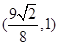 .
.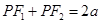 ,
,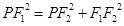 ,
,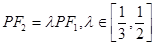 .即可求得
.即可求得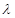 的取值范围.
的取值范围.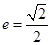 .以及
.以及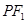 是圆的直径可得
是圆的直径可得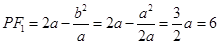 .即可求出椭圆的方程.
.即可求出椭圆的方程.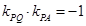 .即得
.即得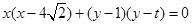 .则M,N所在的直线方程为.两圆方程对减即可得到.根据过定点的知识即可求出定点.本题涉及的知识点较多,渗透方程的思想,加强对几何图形的关系理解.
.则M,N所在的直线方程为.两圆方程对减即可得到.根据过定点的知识即可求出定点.本题涉及的知识点较多,渗透方程的思想,加强对几何图形的关系理解.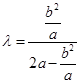 , ∴
, ∴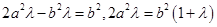 ,
, .
. 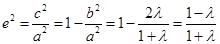 ,∴
,∴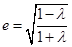 ,在
,在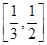 上单调递减.
上单调递减.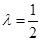 时,
时,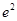 最小
最小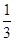 ,
,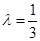 时,
时,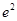 最大
最大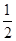 ,∴
,∴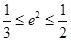 ,∴
,∴ .
.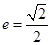 时,
时,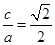 ,∴
,∴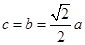 ,∴
,∴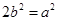 .
.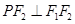 ,∴
,∴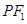 是圆的直径,圆心是
是圆的直径,圆心是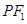 的中点,∴在y轴上截得的弦长就是直径,∴
的中点,∴在y轴上截得的弦长就是直径,∴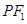 =6.又
=6.又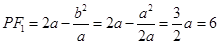 ,∴
,∴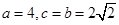 .∴椭圆方程是
.∴椭圆方程是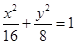 10分
10分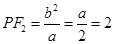 ,于是圆心
,于是圆心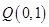 ,半径为3,圆
,半径为3,圆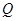 的方程是
的方程是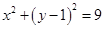 .椭圆的右准线方程为
.椭圆的右准线方程为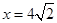 ,,∵直线AM,AN是圆Q的两条切线,∴切点M,N在以AQ为直径的圆上.设A点坐标为
,,∵直线AM,AN是圆Q的两条切线,∴切点M,N在以AQ为直径的圆上.设A点坐标为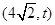 ,∴该圆方程为
,∴该圆方程为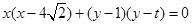 .∴直线MN是两圆的公共弦,两圆方程相减得:
.∴直线MN是两圆的公共弦,两圆方程相减得: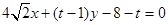 ,这就是直线MN的方程.该直线化为:
,这就是直线MN的方程.该直线化为: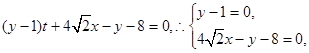
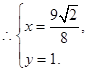
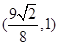 . 16分
. 16分

科目:高中数学 来源:不详 题型:解答题
 经过点
经过点 ,离心率为
,离心率为 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
,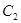 ,若
,若 的实轴是
的实轴是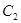 的虚轴,
的虚轴, 的虚轴是
的虚轴是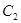 的实轴,则称
的实轴,则称 ,
,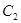 为共轭双曲线.现给出双曲线
为共轭双曲线.现给出双曲线 和双曲线
和双曲线 ,其离心率分别为
,其离心率分别为 .
. 的渐近线方程(不用证明);
的渐近线方程(不用证明); 和双曲线
和双曲线 是否为共轭双曲线?请加以证明.
是否为共轭双曲线?请加以证明. .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
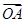 ·
·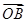 的值;
的值;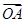 ·
·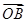 =-4,证明直线l必过一定点,并求出该定点.
=-4,证明直线l必过一定点,并求出该定点.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
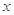 轴上,离心率为
轴上,离心率为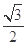 ,长轴长为
,长轴长为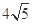 ,直线
,直线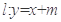 交椭圆于不同的两点
交椭圆于不同的两点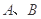 .
.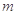 的取值范围;
的取值范围;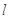 不经过椭圆上的点
不经过椭圆上的点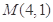 ,求证:直线
,求证:直线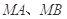 的斜率互为相反数.
的斜率互为相反数.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的左焦点为
的左焦点为 ,离心率为
,离心率为 ,过点
,过点 且与
且与 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为
 的直线
的直线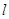 与椭圆交于不同的两点
与椭圆交于不同的两点 ,当
,当 面积最大时,求
面积最大时,求
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
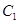 :
: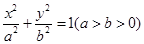 的左、右焦点分别是
的左、右焦点分别是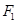 、
、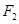 ,下顶点为
,下顶点为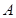 ,线段
,线段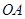 的中点为
的中点为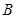 (
(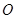 为坐标原点),如图.若抛物线
为坐标原点),如图.若抛物线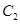 :
: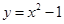 与
与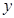 轴的交点为
轴的交点为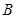 ,且经过
,且经过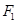 、
、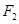 两点.
两点.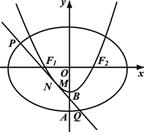
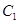 的方程;
的方程;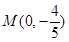 ,
,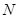 为抛物线
为抛物线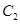 上的一动点,过点
上的一动点,过点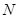 作抛物线
作抛物线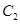 的切线交椭圆
的切线交椭圆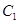 于
于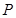 、
、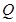 两点,求
两点,求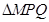 面积的最大值.
面积的最大值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com