
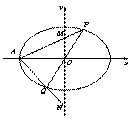
.如图,在平面直角坐标系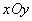 中,离心率为
中,离心率为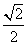 的椭圆
的椭圆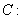
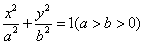 的左顶点为
的左顶点为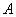 ,过
,过
原点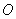 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆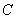 交于
交于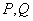 两点,直线
两点,直线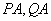 分别与
分别与 轴交于
轴交于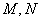 两点.若直线
两点.若直线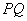 斜率为
斜率为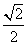 时,
时,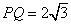 .
.
(1)求椭圆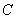 的标准方程; (2)试问以
的标准方程; (2)试问以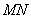 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线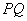 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
科目:高中数学 来源: 题型:
已知双曲线实轴在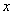 轴,且实轴长为2,离心率
轴,且实轴长为2,离心率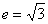 , L是过定点
, L是过定点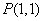 的直线.
的直线.
(1)求双曲线的标准方程;
(2)判断L能否与双曲线交于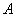 ,
,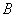 两点,且线段
两点,且线段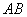 恰好以点
恰好以点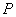 为中点,若存在,求出直线L的方程,若不存,说明理由.
为中点,若存在,求出直线L的方程,若不存,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
某企业2014年2月份生产A、B、C三种产品共6000件,根据分层拍样的结果,该企业统计员制作了如下的统计表格:
| 产品类别 | A | B | C |
| 产品数量 | 2600 | ||
| 样本容量 | 260 |
由于不小心,表格中B、C产品的有关数据已被污染看不清楚,统计员记得B产品的样本容量比C产品的样本容量多20,根据以上信息,可得C的产品数量是 ( )
A.160 B.180 C.1600 D.1800
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合M=N={0,1,2,3},定义函数f:M→N,且点A(0,f(0)), B(i,f(i)),C(i+1,f(i+1)),(其中i=1,2).若△ABC的内切圆圆心为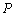 ,且满足
,且满足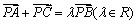 ,则满足条件的
,则满足条件的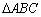 有( )
有( )
A.10个 B.12个 C.18个 D. 24个
查看答案和解析>>
科目:高中数学 来源: 题型:
过抛物线 y2 = 4x 的焦点作直线交抛物线于A(x1, y1)B(x2, y2)两点,如果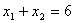
那么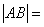 ( )
( )
A. 5 B. 6 C .7 D .8
查看答案和解析>>
科目:高中数学 来源: 题型:
知点(3,1)和(-4,6)在直线3x-2y+a=0两侧,则a的取值范围是( )
A.a<-7或a>24 B.a=7或a=24 C.-7<a<24 D.-24<a<7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com