
已知函数f (x)
= 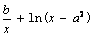
(1)若函数y = f (x)存在零点a2 + 1,且直线y = x – 1与函数y = f (x)的图象相切,求a的值.
(2)当b = 1时,讨论f (x)的单调性.
【解析】(1)由f (a2 + 1) = 0得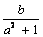 + ln1= 0,∴
+ ln1= 0,∴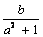 = 0即b = 0.设直线y = x–1与曲线y = f (x)切点为P(x0,y0),则
= 0即b = 0.设直线y = x–1与曲线y = f (x)切点为P(x0,y0),则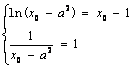 ,
,
∴x0 – a2 = 1,∴x0 – 1 = 0,x0 = 1,∴a = 0.……5分
(2)b = 1时,f (x)
= 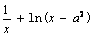 ,f (x)定义域为(a2,+∞).
,f (x)定义域为(a2,+∞).
f′(x)
= 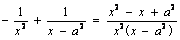 ,设h (x) = x2 – x + a2,二次方程h (x) = 0对应的判别式
,设h (x) = x2 – x + a2,二次方程h (x) = 0对应的判别式 = 1 – 4a2.……6分
= 1 – 4a2.……6分
①当 <0即a>
<0即a>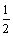 或a<–
或a<–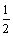 时,对一切x>a2,都有f′(x)>0,此时f (x)是(a2,+∞)上的单调递增函数.……7分
时,对一切x>a2,都有f′(x)>0,此时f (x)是(a2,+∞)上的单调递增函数.……7分
②当 =0即a =±
=0即a =±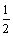 时,仅对x =
时,仅对x = 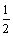 有f′(x) = 0,对于其余的x>a2都有f′(x)>0.此时f (x)是(a2,+∞)上的单调递增函数.……8分
有f′(x) = 0,对于其余的x>a2都有f′(x)>0.此时f (x)是(a2,+∞)上的单调递增函数.……8分
③当 >0即–
>0即–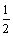 <a<
<a<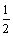 时,方程h (x) = 0有两个不同实根x1 =
时,方程h (x) = 0有两个不同实根x1 = 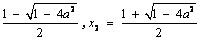 ,a2<x1<x2,f (x),f′(x)随x的变化如下表.
,a2<x1<x2,f (x),f′(x)随x的变化如下表.
|
x |
(a2,x1) |
x1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
f′(x) |
+ |
0 |
– |
0 |
+ |
|
f (x) |
↑ |
极大值 |
↓ |
极小值 |
↑ |
此时y=f (x)在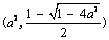 上单调递增,在
上单调递增,在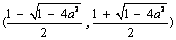 上单调递减.在
上单调递减.在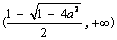 上单调递增. ……13分
上单调递增. ……13分


科目:高中数学 来源: 题型:
|
| 1 |
| π |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| x-1 | x+a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com