
| A. | [1,e-1] | B. | {1}∪($\frac{1}{e}$+1,e-1] | C. | [1,$\frac{1}{e}$+1] | D. | ($\frac{1}{e}$+1,e-1] |
分析 根据题意便可知道方程lnx=x-a在$[\frac{1}{e},e]$上有唯一的解,进而可看成y=lnx与y=x-a在$[\frac{1}{e},e]$上存在唯一的公共点,并可画出图象,容易求出两函数图象相切时,a=1,并可求出当直线y=x-a过$A(\frac{1}{e},-1)$,B(e,1)时a的值,这样便可结合图象求出实数a的取值范围.
解答 解:据题意,两个函数图象上恰好存在唯一一个关于x轴对称的点,
即点(x,y)与(x,-y)分别在两个函数图象上,且唯一;
又$\frac{1}{e}≤x≤e$,则:
$\left\{\begin{array}{l}{y=f(x)=lnx}\\{y=-g(x)=x-a}\end{array}\right.$,即方程,lnx=x-a在$[\frac{1}{e},e]$上有唯一一解;
∴可化归为y=lnx的图象和直线y=x-a当$x∈[\frac{1}{e},e]$时有唯一的公共点;
如图,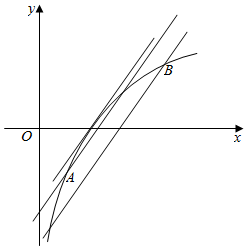
①当两函数图象相切时,设切点(x0,y0),$y′=(lnx)′=\frac{1}{x}$;
∴$y′{|}_{x={x}_{0}}=\frac{1}{{x}_{0}}=1$,x0=1;
∴切点为(1,0),带入直线方程得a=1;
②当直线y=x-a过点$A(\frac{1}{e},-1)$时,a=$\frac{1}{e}+1$,当直线y=x-a过点B(e,1)时,a=e-1,
结合图象可知恰好存在唯一一个关于x轴对称的点,则:a=1或$\frac{1}{e}+1<a≤e-1$.
故选B.
点评 考查关于x轴对称的点的坐标关系,以及方程的解和对应函数图象的关系,函数在图象上一点的导数值和过该点切线斜率的关系,以及数形结合解决问题的方法.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
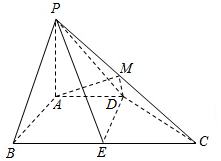 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=PB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC的中点,点E为BC边上的点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,PA=PB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC的中点,点E为BC边上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
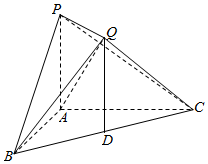 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=1,AB=AC=$\sqrt{2}$,D为BC的中点,过点D作DQ∥AP,且DQ=1,连结QB,QC,QP.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=1,AB=AC=$\sqrt{2}$,D为BC的中点,过点D作DQ∥AP,且DQ=1,连结QB,QC,QP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com