
分析 (1)求出函数的导数,求出a的值,计算f′(1),f(1)的值,代入切线方程即可;
(2)令g(x)=-x2+(2-a)x+a,得到当x≥2时a≥$\frac{{-x}^{2}+2x}{x-1}$,令h(x)=$\frac{{-x}^{2}+2x}{x-1}$=-(x-1)+$\frac{1}{x-1}$,通过换元法结合函数的单调性求出h(x)的最大值,从而求出a的范围即可.
解答 解:(1)f′(x)=$\frac{{-x}^{2}+(2-a)x+a}{{e}^{x}}$,
依条件f′(0)=0,
∴a=0,
此时,f(x)=$\frac{{x}^{2}}{{e}^{x}}$,f′(x)=$\frac{-x(x-2)}{{e}^{x}}$,
∴f′(1)=$\frac{1}{e}$,切点(1,$\frac{1}{e}$),
∴切线方程为:x-ey=0;
(2)令g(x)=-x2+(2-a)x+a,
依条件g(x)≤0在[2,+∞)上恒成立,
∴-x2+(2-a)x+a≤0,
∴(x-1)a≥-x2+2x,
当x≥2时a≥$\frac{{-x}^{2}+2x}{x-1}$,
令h(x)=$\frac{{-x}^{2}+2x}{x-1}$=-(x-1)+$\frac{1}{x-1}$,
令x-1=t(t≥1),
∴h(x)=-t+$\frac{1}{t}$=F(t),
F′(t)=-1-$\frac{1}{{t}^{2}}$<0,
∴F(t)在(1,+∞)递减,
∴h(x)max=F(1)=0,
∴a≥0.
点评 本题考查了导数的运算法则、利用导数的几何意义研究切线方程、利用导数研究函数的单调性极值,考查了分类讨论思想方法、“分离参数法”、推理能力与计算能力


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,e-1] | B. | {1}∪($\frac{1}{e}$+1,e-1] | C. | [1,$\frac{1}{e}$+1] | D. | ($\frac{1}{e}$+1,e-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 天数t(天) | 3 | 4 | 5 | 6 | 7 |
| 繁殖个数y(千个) | 5 | 6 | 8 | 9 | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 二月上旬 | 二月中旬 | 二月下旬 | 三月上旬 |
| 旬平均气温x(℃) | 3 | 8 | 12 | 17 |
| 旬销售量y(件) | 55 | m | 33 | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 时间代号x | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y (千亿元) | 5 | 6 | 7 | 8 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
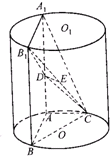 如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,且AB=AC=$\frac{1}{2}$AA1=2.
如图,AA1,BB1为圆柱OO1的母线,BC是底面圆O的直径,D、E分别是AA1、CB1的中点,且AB=AC=$\frac{1}{2}$AA1=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com