
| 时间 | 二月上旬 | 二月中旬 | 二月下旬 | 三月上旬 |
| 旬平均气温x(℃) | 3 | 8 | 12 | 17 |
| 旬销售量y(件) | 55 | m | 33 | 24 |
分析 (1)由样本中心点$\overline{y}$=38,根据平均值的定义,即可求得m的值;
(2)根据样本中心点一定在线性回归方程上,求出a的值,写出线性回归方程.当x=22时,代入回归直线方程,进而利用方程进行预测.
解答 解:(1)由样本中心点为(10,38).即$\overline{y}$=38,
由$\overline{y}$=$\frac{55+m+33+24}{4}$=38,解得m=40,
(2)由(1)可知线性回归方程y=-2x+$\widehat{a}$,过样本中心点,
$\widehat{a}$=$\overline{y}$+2$\overline{x}$=38+2×10=58,
故回归直线方程为:y=-2x+58;
当x=22时,y=14,
故三月中旬的平均气温约为22℃时,该品牌的保暖衬衣在三月中旬的销售量14件.
故(1)答案为:40.
点评 本题考查线性回归方程,考查利用线性回归方程进行预测,属于基础题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
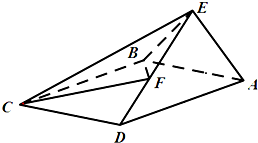 如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=1,AE⊥平面CDE,$AE=DE=\sqrt{6}$,F为线段DE上的一点.
如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=1,AE⊥平面CDE,$AE=DE=\sqrt{6}$,F为线段DE上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | (0,1) | C. | [1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
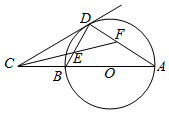 如图,AB是圆O的直径,C为AB的延长线上一点,切线CD交圆O于点D,∠ACD的平分线分别交DB,DA于点E,F.
如图,AB是圆O的直径,C为AB的延长线上一点,切线CD交圆O于点D,∠ACD的平分线分别交DB,DA于点E,F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x | 9 | 9.5 | 10.5 | 11 |
| 销售量y | 11 | 10 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | mf(xn)>nf(xm) | B. | mf(xn)<nf(xm) | ||
| C. | mf(xn)=nf(xm) | D. | mf(xn)与nf(xm)大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正四棱锥S-ABCD的底面边长为2,E,F分别为SA,SD的中点.
如图,正四棱锥S-ABCD的底面边长为2,E,F分别为SA,SD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com