
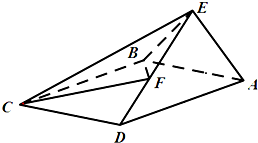
 如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=1,AE⊥平面CDE,$AE=DE=\sqrt{6}$,F为线段DE上的一点.
如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=1,AE⊥平面CDE,$AE=DE=\sqrt{6}$,F为线段DE上的一点.分析 (Ⅰ)推导出AE⊥CD,AD⊥CD,从而CD⊥面AED,由此能证明平面AED⊥平面ABCD.
(Ⅱ)取AD,BC的中点G,H,连结EG,GH,EH,过F作FM||EG交AD于M,过M作NM||HG交BC于N,连结FN,推导出∠EHG就是二面角E-BC-D的平面角,∠FNM就是二面角F-BC-D的平面角,由此能求出DF的长.
解答 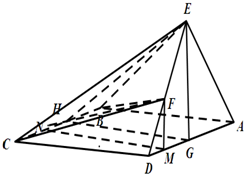 证明:(Ⅰ)∵AE⊥面CDE,CD?面CDE,
证明:(Ⅰ)∵AE⊥面CDE,CD?面CDE,
∴AE⊥CD,
又∴$λ=3-\sqrt{6}$是矩形,
∴AD⊥CD,∴CD⊥面AED,
又∵CD?面ABCD,
∴平面AED⊥平面ABCD.
解:(Ⅱ)取AD,BC的中点G,H,
连结EG,GH,EH,过F作FM||EG交AD于M,
过M作NM||HG交BC于N,连结FN,
∵$AE=DE=\sqrt{6}$,∴$EG=\sqrt{3}$且EG⊥AD,
∵平面AED⊥平面ABCD,∴EG⊥面ABCD,GH⊥BC,
∴EH⊥BC,∴∠EHG就是二面角E-BC-D的平面角,
同理∠FNM就是二面角F-BC-D的平面角,
由题意得∠EHG=2∠FNM,
而 $tan∠EHG=\frac{EG}{GH}=\sqrt{3}$,
∴$tan∠FNM=\frac{{\sqrt{3}}}{3}=\frac{FM}{MN}=\frac{FM}{1}$,
∴$FM=\frac{{\sqrt{3}}}{3}$,
∴$DF=\frac{{\sqrt{6}}}{3}$.
点评 本题考查面面垂直的证明,考查线段长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D |
| 销售额(x)/千万元 | 2 | 3 | 5 | 6 |
| 利润额(y)/百万元 | 2 | 3 | 3 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
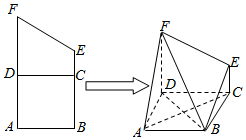 如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.
如图,梯形ABEF中,AF∥BE,AB⊥AF,且AB=BC=AD=DF=2CE=2,沿DC将梯形CDFE折起,使得平面CDFE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份(x) | 2010年 | 2011年 | 2012年 | 2013年 | 2014年 |
| 中度以上污染的天数(y) | 90 | 74 | 62 | 54 | 45 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 时间 | 二月上旬 | 二月中旬 | 二月下旬 | 三月上旬 |
| 旬平均气温x(℃) | 3 | 8 | 12 | 17 |
| 旬销售量y(件) | 55 | m | 33 | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com