
分析 根据同角的三角函数关系与二倍角的公式,进行计算即可.
解答 解:因为α为第四象限角,
所以sinα<0,cosα>0,
从而sinα-cosα<0,
由cosα-|sinα-cosα|=-$\frac{3}{5}$,
得cosα-(cosα-sinα)=-$\frac{3}{5}$,即sinα=-$\frac{3}{5}$;
所以cosα=$\sqrt{1{-sin}^{2}α}$-$\sqrt{1{-(-\frac{3}{5})}^{2}}$=$\frac{4}{5}$;
tanα=$\frac{sinα}{cosα}$=$\frac{-\frac{3}{5}}{\frac{4}{5}}$=-$\frac{3}{4}$;
sin2α=2sinαcosα=2×(-$\frac{3}{5}$)×$\frac{4}{5}$=-$\frac{24}{25}$;
cos2α=2cos2α-1=2×${(\frac{4}{5})}^{2}$-1=$\frac{7}{25}$.
点评 本题考查了同角的三角函数关系与二倍角的公式与应用问题,也考查了计算求值问题,是基础题目.


科目:高中数学 来源: 题型:解答题
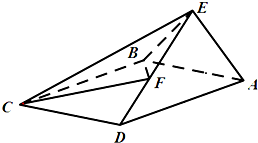 如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=1,AE⊥平面CDE,$AE=DE=\sqrt{6}$,F为线段DE上的一点.
如图,在四棱锥E-ABCD中,底面ABCD是矩形,AB=1,AE⊥平面CDE,$AE=DE=\sqrt{6}$,F为线段DE上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x | 9 | 9.5 | 10.5 | 11 |
| 销售量y | 11 | 10 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | mf(xn)>nf(xm) | B. | mf(xn)<nf(xm) | ||
| C. | mf(xn)=nf(xm) | D. | mf(xn)与nf(xm)大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.
AB是⊙O的直径,点C是⊙O上的动点,过动点C的直线VC垂直于⊙O所在的平面,D,E分别是VA,VC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正四棱锥S-ABCD的底面边长为2,E,F分别为SA,SD的中点.
如图,正四棱锥S-ABCD的底面边长为2,E,F分别为SA,SD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com