
【题目】如图,在四边形ACBD中, ![]() ,且△ABC为正三角形.
,且△ABC为正三角形.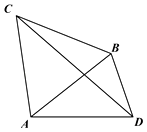
(Ⅰ)求cos∠BAD的值;
(Ⅱ)若CD=4, ![]() ,求AB和AD的长.
,求AB和AD的长.
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() 的离心率为
的离心率为 ![]() ,且经过点M
,且经过点M ![]() 的直径C1的长轴.如图,C是椭圆短轴端点,动直线AB过点C且与圆C2交于A,B两点,CD垂直于AB交椭圆于点D.
的直径C1的长轴.如图,C是椭圆短轴端点,动直线AB过点C且与圆C2交于A,B两点,CD垂直于AB交椭圆于点D. 
(1)求椭圆C1的方程;
(2)求△ABD面积的最大值,并求此时直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 , CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[﹣2,2]上的奇函数,且f(2)=3,若对任意的m,n∈[﹣2,2],m+n≠0,都有 ![]() >0.
>0.
(1)若f(2a﹣1)<f(a2﹣2a+2),求实数a的取值范围;
(2)若不等式f(x)≤(5﹣2a)t+1对任意x∈[﹣2,2]和a∈[﹣1,2]都恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知非空集合A,B满足以下两个条件.
(ⅰ)A∪B={1,2,3,4,5,6},A∩B=;
(ⅱ)A的元素个数不是A中的元素,B的元素个数不是B中的元素,则有序集合对(A,B)的个数为( )
A.10
B.12
C.14
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2+x﹣a.a∈R
(1)若不等式f(x)<b的解集为(﹣∞,﹣1)∪(3,+∞),求a,b的值;
(2)若a<0,解不等式f(x)>1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() .
.
(1)求f(x)的周期及其图象的对称中心;
(2)△ABC中,角A、B、C所对的边分别是a、b、c,满足(2a﹣c)cosB=bcosC,求f(B)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com