
���� ������Ϊ��ÿ����̨ÿСʱ6Ԫ�����շ�Ϊf��x����x�����������ã�f��x��=6x�������÷ֶκ����ı���ʽ���������g��x���ı���ʽ��
��II������֪��С��ѡ���ļұȽϺ��㣬�ؼ��ǿ���һ���շѵͣ���ֻҪ�Ƚ�f��x�� ��g��x���ĺ����Ĵ�С���ɣ����ѡ����õ͵�һ�Ҽ��ɣ�
��� �⣺����f��x��=6x����12��x��40����
g��x��=$\left\{\begin{array}{l}{90����12��x��30��}\\{2x+50����20��x��30��}\end{array}\right.$��
��II����x=15ʱ��f��x��=g��x������15��x��30ʱ��f��x��-g��x��=6x-��2x+50��=3x-50��0��
��f��x����g��x����ѡ�Ҽң�
���� ���ʵ������ͨ�����ĸ����裺��1���Ķ����⣬�������⣻��2��������ѧ���ţ�������ѧģ�ͣ���3��������ѧ�ķ������õ���ѧ�������4��ת��ɾ�����������������йؼ��ǽ�����ѧģ�ͣ��ֶκ���������ԣ��ֶκ���ģ�͵Ĺ����У��Ա���ȡֵ�ķֽ��ǹؼ��㣬ֻ�к����ķ��࣬��ȷ�������ܳɹ��ؽ��⣮������ʱҪ�������ز�©��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
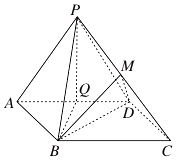 ��ͼ���߳�Ϊ4��������ABCD����ƽ������������PAD����ƽ�滥�ഹֱ��M��Q�ֱ�ΪPC��AD���е㣮
��ͼ���߳�Ϊ4��������ABCD����ƽ������������PAD����ƽ�滥�ഹֱ��M��Q�ֱ�ΪPC��AD���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | �٢� | B�� | �ڢ� | C�� | �ڢ� | D�� | �ۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 1 | C�� | -1 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 0 | C�� | -1 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x^2}{16}+\frac{y^2}{32}=1$ | B�� | $\frac{x^2}{32}+\frac{y^2}{4}=1$ | C�� | $\frac{x^2}{32}+\frac{y^2}{16}=1$ | D�� | $\frac{x^2}{64}+\frac{y^2}{32}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ˫���� | B�� | ˫���ߵ���֧ | C�� | ˫���ߵ���֧ | D�� | Բ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com